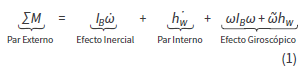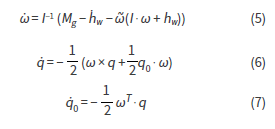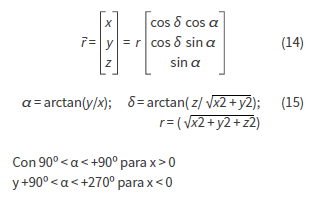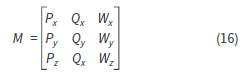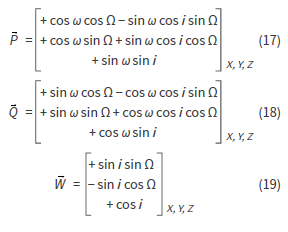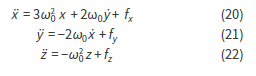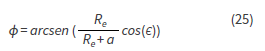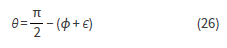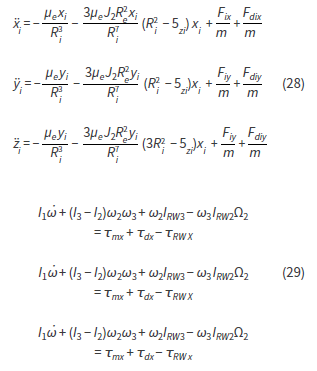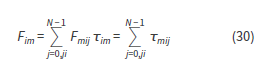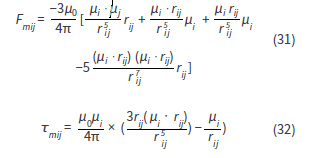Tecnología e Innovación
Ciencia y Poder Aéreo ISSN 1909-7050 / E-ISSN 2389-9468 / volumen 15 (2) julio-diciembre del 2020 / Colombia / pp. 143-165 / https://doi.org/10.18667/cienciaypoderaereo.678
Diseño de misión, síntesis de factores operacionales y representaciones del segmento espacial, caso FACSAT y EMFF
Mission Design and Synthesis of Operational Factors and Representations of the Space Segment: The Case of FACSAT and EMFF
Desenho de missão e sínteses de fatores operacionais e representações do segmento espacial, Caso-FACSAT y EMFF
Fecha de recibido: 06 de abril del 2020 | Fecha de aprobación: 19 de septiembre del 2020
Germán Wedge Rodríguez-Pirateque
Magíster en Ingeniería Mecánica y Mecatrónica
Jorge Sofrony Esmeral
Ph. D. en Sistemas de Control
Ernesto David Cortés García
Ingeniero Mecatrónico
Kennet Rueda
Estudiante de Física
Resumen:
el presente artículo tiene como propósito el análisis del segmento espacial como parte del proceso de estructuración de un proyecto aeroespacial, partiendo del problema de desarticulación de procesos de diseño, omisión de factores operacionales y desconocimiento del comportamiento del segmento espacial en órbita. Para esto es necesario el recuento de los pasos requeridos en el diseño de misión de un sistema espacial, la arquitectura y subsistemas constitutivos del segmento genérico e identificación de factores operacionales útiles para el desarrollo del concepto de misión. Adicionalmente, se presentan diferentes formas de representación del movimiento de orientación y traslación del segmento espacial, como guía para el modelamiento de misiones de observación terrestre en órbita baja. Con base en esto se obtienen dos caracterizaciones como ejemplos prácticos para las necesidades de diseño y representación, tanto para el diseño de misión con la síntesis de objetivos de misión de un programa espacial, como para la representación del segmento espacial, frente a las necesidades de uso de un arreglo de misión de gran proximidad y con capacidades de maniobra en órbita, que incluso, pueda requerir no solo uno sino varios satélites en coordinación, todo esto mediante el modelo de vuelo de formación electromagnética (EMFF).
Palabras clave: diseño de misión; EMFF; FACSAT; factores operacionales; orientación y traslación satelital; segmento espacial; subsistemas CubeSat.
Abstract:
This article examines the space segment as part of the structuring process of an aerospace project, starting from the problem of disarticulation of design processes, the omission of operational factors, and unawareness of the behavior of the space segment in orbit. For this purpose, it is necessary to revisit the steps required in the mission design of a space system, the architecture and the constituent subsystems of the generic segment, as well as the useful operational factors for the development of the mission concept. Hence, different representations of the orientation and translation movement of the space segment are presented as a guide for the modeling of low-orbit observation missions. Based on this, two characterizations of design and representation requirements are provided as practical examples —both for the mission design, with the synthesis of mission objectives of a space program, and the representation of the space segment— against the needs of a close proximity mission with inorbit maneuvering capabilities that may require not one but several coordinated satellites; all this by using the Electromagnetic Formation Flying method (EMFF).
Keywords: Mission design; space segment; EMFF; FACSAT; operational factors; satellite orientation and translation; CubeSat subsystems.
Resumo:
O artigo tem como objetivo a análise do segmento espacial como parte do proscesso de estruturação de um projeto aeroespacial, partindo do problema da desarticulação de processos de design, omissão de fatores operacionais e o desconhecimento do comportamento do segmento espacial em órbita. Para isso, é necessário contabilizar as etapas requeridas no desenho de missão de um sistema espacial, a arquitetura e subsistemas constitutivos do segmento genérico, e a identificação de fatores operacionas úteis para o desenvolvimento do conceito de missão. Além disso, diferentes formas de representação do movimento de orientação e translação do segmento espacial são apresentadas como modelo para a modelagem de missões de observação terrestre em órbita baixa. Com base nisso, duas caracterizações são obtidas como exemplos práticos das necessidades de design e representação, tanto para o design de missão com a síntese dos objetivos da missão de um programa espacial, quanto para a representação do segmento espacial, voltada para as necessidades de uso de um ajuste de missão de grande proximidade e com capacidades de manobra em órbita que pode mesmo precisar não apenas um, mas vários satélites coordenados, tudo isso usando o modelo de vôo de treinamento eletromagnético.
Palavras-chave: Desenho de missão; Segmento espacial; EMFF; FACSAT; Fatores operacionais; Orientação e translação satelital; Subsistemas CubeSat.
Introducción
Las misiones de observación terrestre son uno de los servicios aeroespaciales más significativos y solicitados en el uso de sistemas satelitales a lo largo de su implementación, razón por la cual se hace necesario su estudio y comprensión desde el proceso del diseño de misión (Álvarez-Reyna et al., 2019), hasta los factores operacionales y los modelos matemáticos disponibles para representar el sistema. Para esto, es conveniente partir de la diferenciación de cada uno de los segmentos que componen el sistema espacial como lo ilustra la figura 1, donde se destacan: el segmento terrestre (Estación terrena y redes de apoyo), el segmento de lanzamiento (Base, plataforma y sistemas de lanzamiento), el segmento de comando y control (Enlace), el segmento espacial (satélites y vehículos autónomos) y el segmento de usuario (Cliente y entidades aliadas) (Xu et al., 2018).
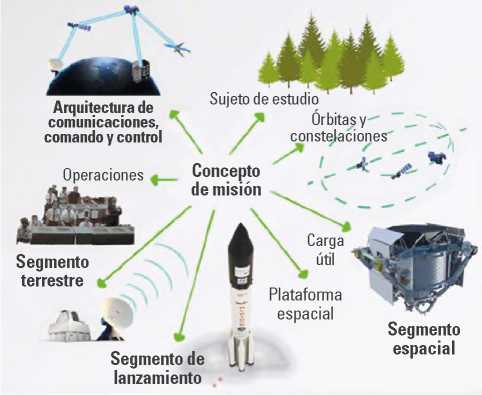 Figura 1. Sistema espacial
Figura 1. Sistema espacial
Fuente: Agencia Espacial Mexicana (2013).
Es preciso aclarar que previo al análisis de factores operacionales, es necesario introducir el concepto de “diseño de misión”, el cual permite visualizar y planear el proyecto espacial como un todo, para ser caracterizado y evaluado mediante un proceso en el que se configuren cada uno de los segmentos de acuerdo al servicio aeroespacial requerido (Burleigh et al., 2019). Con base en esta formulación del diseño de misión, se puede avanzar entonces en el análisis de requisitos y operación del satélite como segmento espacial que debe ser controlado y aprovechado en el tiempo de su vida útil.
Por ejemplo, en misiones de imágenes satelitales, donde se requiere un control de orientación que permita a cada satélite apuntar adecuadamente a un objetivo en tierra. Otro ejemplo son las misiones de gran proximidad, como la Misión nodes para toma de imágenes del Small Spacecraft Technology Program-NASA (SSTP) o las misiones Experimental Spacecraft System (XSS), XSS-10 & XSS-11 de la us Air Force Research Laboratory (AFRL), las cuales requieren que el conjunto de satélites mantenga una formación cercana y a la vez realicen movimientos orbitales de alta velocidad, lo que exige sistemas de alta confiabilidad y desempeño.
También es ejemplo de misión el laboratorio de investigaciones de la Fuerza Aérea de los Estados Unidos, que por medio de su programa TechSat21, con la empresa DARPA y otras 10 universidades americanas, trabajaron en el desarrollo del concepto de Nano-Satélites y lograron realizar el lanzamiento de 10 Nano-Satélites, a partir de un diseño de misión en cuatro pasos.
La operación del FormSat (Braukhane et al., 2010) con su modelo de negocio en torno a la operación de servicios satelitales y de manufactura permite disponer diferentes cargas útiles para cada servicio, o el proyecto SAMSON mediante el cual se presenta un modelo de vuelo de clúster satelitales con la geolocalización de tres nanosatélites dentro de un segmento espacial, segmento de Tierra, segmento de usuario y segmento de lanzamiento (Gurfil et al., 2012).
En este sentido, además de la representación de los segmentos espaciales descritos sobre una órbita específica o una topología dada (Blasch et al., 2014), también es importante considerar dentro de una misión, los demás componentes del sistema satelital, como las estaciones en Tierra y los propios objetivos en Tierra hacia donde estarían focalizadas las misiones de los agentes satelitales (Mazal & Gurfil, 2014).
De acuerdo con esto y con la composición del sistema espacial (Larson & Wertz, 1999), el presente documento se enfoca específicamente en el segmento espacial, es decir, el artefacto o nave espacial puesta en órbita (satélite), con el fin de identificar los factores que inciden en su operación y desempeño, así como algunos de los modelos matemáticos disponibles para representarlo como un medio práctico para la observación terrestre, particularmente en órbitas bajas (LEO) (Mingqi et al., 2017).
Para el análisis de estos fines, el artículo se estructura en las siguientes secciones: la sección i, presenta los pasos para el diseño de una misión, necesarios para abordar proyectos y necesidades en servicios aeroespaciales, así como los factores operacionales que influyen en el desempeño del segmento espacial, considerando la arquitectura y subsistemas de un satélite; la sección ii, presenta diferentes tipos de representación con las que el segmento espacial puede ser analizado y simulado en pruebas de seguimiento; la sección iii, detalla con dos ejemplos tanto el primer paso del diseño de misión con un programa espacial, como la aplicación de las formas de representación en el movimiento traslacional, los cuales se realizan con la formulación y simulación del sistema EMFF, con el que se demuestra la operación de uno o varios satélites en órbita con sistemas de actuación para su traslación en la órbita. Y por último, en la sección IV, se presentan las conclusiones y recomendaciones para trabajos futuros.
Diseño de misión y factores operacionales
El diseño de misión es uno de los requisitos fundamentales a la hora de abordar proyectos que involucren servicios aeroespaciales, su estructuración y seguimiento permite la adecuada configuración de objetivos y el potencial éxito en el desarrollo e implementación de las soluciones planteadas. Para esto se toma como referencia el siguiente proceso de diseño, con la base teórica clásica, que a la fecha sigue siendo vigente en su implementación y desarrollo (Larson & Wertz, 1999).
Pasos del diseño de misión
De acuerdo al análisis y diseño de misiones espaciales (SMAD-ESA) (Marsden, 2002), el diseño de una misión consta de los siguientes pasos:
1. Definir objetivos
-
a. Definir objetivos generales y limitaciones.
b. Estimar las necesidades y requisitos cuantitativos de la misión.
2. Caracterizar la misión
-
a. Definir conceptos alternativos de misión.
-
b. Definir arquitecturas alternativas de misión.
-
c. Identificar los controladores del sistema.
-
d. Caracterizar conceptos y arquitecturas de misión.
3. Evaluar la misión
-
a. Identificar requisitos críticos.
-
b. Evaluar la utilidad de la misión.
-
c. Definir el concepto de misión base.
4. Definir requisitos
a. Definir requisitos del sistema:
- i. Funcionales
- ii. Operativos
- iii. Restricciones
b. Asignar requisitos a elementos del sistema.
El seguimiento y apropiación de cada uno de los pasos dan la claridad y asertividad en la definición de misiones con todo lo que implica la gestión, administración, operación y composición de los segmentos. De esta forma se puede precisar la configuración de equipos, logística, personal, subsistemas y desempeño de cada segmento para su operación y mantenimiento en el tiempo de funcionamiento.
El proceso de diseño de misión se materializa mediante la formulación de programas, y a su vez, la definición de proyectos que respondan a las necesidades planteadas, teniendo como base las siguientes fases del ciclo de vida de un proyecto del orden aeroespacial como lo han desarrollado ampliamente las agencias espaciales más representativas del mundo (NASA, 2007).
Adquisiciones presistema
1. Prefase-A / evaluación de conceptos
- Borrador de los requerimientos del proyecto.
- Revisión del concepto de la misión (Mission Concept Review –MCR–).
2. Fase A / desarrollo de concepto y tecnología
- Plan de proyecto preliminar.
- Revisión de los requerimientos del sistema (Systems Requirements Review –SRR–).
- Revisión de la definición de la misión (Mission Definition Review –MDR–).
3. Fase B / diseño preliminar y definición tecnológica
- Plan de proyecto de línea base.
- Preliminar (Preliminary Design Review -PDR-).
Adquisiciones del sistema
1. Fase C / diseño final y fabricación
- Revisión crítica del diseño (Critical Design Review –CDR–).
- Revisión de las interfaces del sistema (System Interface Review –SIR–).
2. Fase D / ensamblaje del sistema, integración y prueba, lanzamiento
- Revisión de preparación operacional (Operational Readiness Review –ORR–).
- Revisión previa del transporte antes de llegar al sitio de lanzamiento (Review prior to shipment to launch site –PRE-SHIP–).
Operaciones
1. Fase E / operaciones y sostenimiento
- Fin de misión.
- Revisión de preparación de vuelo (Flight Readiness Review -FRR-).
- Revisión de preparación de lanzamiento (Launch Readiness Review -LRR-).
- Revisión de valoración post lanzamiento (Post Launch Assessment Review -PLAR-).
- Revisión de preparación de eventos críticos(Critical Events Readiness Review -CERR.-)
Retiro de servicio
1. Fase F / cierre y recuperación
- Archivo final de datos.
- Revisión de retiro de servicio (Decomissioning Review -DR-).
Con base en estas fases del proyecto se realiza la descomposición del sistema por niveles y se determinan los recursos y materiales necesarios mediante las siguientes líneas de trabajo y despliegue de funciones, con las cuales se puntualizan las acciones y se asigna la responsabilidad a cada uno de los actores en el análisis, diseño, desarrollo, implementación y evaluación de los proyectos frente a sus objetivos y resultados esperados:
-
2. Ingeniería de sistemas
-
3. Control de calidad
-
4. Manejo de datos
-
5. Carga útil
-
6. Bus satelital
-
7. Operaciones
-
8. Lanzamiento
-
9. Sistemas de tierra
-
10. Integración y verificación
-
11. Educación y divulgación
1. Gestión del proyecto
Como complemento a los procesos de análisis y gestión de proyectos, es importante considerar los diferentes factores operacionales al momento de plantear cada paso del diseño de misión, para visualizar los posibles problemas y alternativas de funcionabilidad. Desde la misma arquitectura y subsistemas del satélite que se deben tener en cuenta para la formulación de la misión, como lo ilustra la figura 2.
Factores operacionales
Los factores operacionales se abordan desde la descripción física de los satélites, como punto de partida para entender el comportamiento de los equipos en órbita. Los movimientos de traslación y orientación con los cuales se posicionan los satélites, son determinantes para una correcta toma de imágenes, lo cual se logra al reconocer, dentro de la arquitectura del segmento espacial, los diferentes subsistemas con los cuales el satélite afronta los requerimientos de la misión (figura 2):
 Figura 2. Arquitectura y subsistemas de un CubeSat
Figura 2. Arquitectura y subsistemas de un CubeSat
Fuente: Radhakrishnan et al. (2016).
Los subsistemas representados en la arquitectura del segmento espacial, se componen de dos secciones funcionales principales, la primera incluye todo lo relacionado con la carga útil —también llamado sensor del satélite— y la segunda sección denominada el bus satelital, donde se alojan los demás bloques funcionales del sistema, tales como el computador a bordo (OBC), potencia, térmico y estructura, comunicaciones, propulsión y en especial, el subsistema de control y determinación de actitud (ADCS).
Cada uno de estos subsistemas aporta requerimientos a la misión y adicionan dinámicas propias al modelo físico del agente. Se destacan el subsistema adcs para el problema de orientación y el subsistema de propulsión para el problema de traslación cuando se cuenta con este medio de desplazamiento alternativo en misiones de maniobras más allá del eje de rotación o plano orbital del agente.
El abordaje de estos desplazamientos parte de herramientas básicas de la mecánica newtoniana y la mecánica celeste, así como de representaciones útiles para diferenciar los marcos de referencia de los objetos, ya sea como partículas o como cuerpos en el espacio. Esto dependiendo el nivel de detalle que se quiera plantear para la descripción de los movimientos y de los demás factores y condiciones del medio donde se desenvuelve el segmento espacial.
La caracterización técnica, tanto de las cargas útiles como de los subsistemas del bus satelital está dada por la definición de capacidades de los elementos del software y hardware (Navarro, 2016), tal como se muestra en la tabla 1:
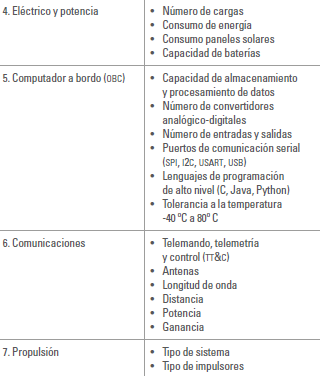 Tabla 1. Características técnicas por subsistema CubeSat
Tabla 1. Características técnicas por subsistema CubeSat
Fuente: elaboración propia.
A partir de estas descripciones se despliega el análisis de factores que desde el punto de vista físico pueden afectar el desempeño y prestación de los servicios de observación terrestre, como es el caso de la precisión de apuntamiento o el seguimiento de órbita, para los cuales cada subsistema aporta al cumplimiento de los objetivos de misión.
Identificación de factores
La síntesis de factores refiere la identificación y puesta en contexto de aquellas limitaciones, perturbaciones, mediciones y características de operación, frente a las cuales se ve sometido el segmento espacial, particularmente la incidencia que estos causan sobre la estabilidad y el control de los equipos satelitales en órbita.
Además, independiente al comportamiento del satélite existen limitaciones y parámetros asociados que abren la ventana de incógnitas sobre el desempeño de los equipos y el cumplimiento de las misiones para las cuales fueron diseñados. Algunos de estos parámetros se presentan en la tabla 2.
Tabla 2.Limitaciones de operación satelital
En términos generales algunos de los parámetros más significativos para el desempeño de un satélite de observación terrestre son los siguientes:
1. Satélite
-
a. Resolución (pancromático y color).
b. Ancho de barrido (en inglés swath).
c. Variedad de modos (franja, mosaico, amplia cobertura, puntual o en inglés spot).
-
d. Agilidad.
-
e. Precisión en navegación.
-
f. Actitud angular.
-
g. Ángulo máximo de desviación (en inglés tilt angle).
-
h. Tiempo de toma de imagen.
-
i. Cobertura terrena (en inglés ground coverage).
-
j. Capacidad de memoria a bordo.
k. Velocidad de transmisión de resultados de la misión.
2. Órbita
-
a. Tipo de órbita (altura e inclinación, por ejemplo, sun-synchronic, órbita anclada, en inglés locked orbit).
b. Tiempo de revisita.
c. Elección del objetivo según su prioridad (por ejemplo, un satélite puede fotografiar dos objetivos, elegir qué tiene prioridad más alta).
3. Estación terrena
-
a. Tiempo de recepción y procesamiento inicial.
b. Procesamiento de imagen: tiempo y calidad.
c. Tiempo de diseminación de los productos (imágenes). Se pueden usar estaciones terrenas que trabajan en red, que reciben los resultados de la misión, según las prioridades de las misiones.
Por otra parte, para los parámetros asociados a satélites en red como es el caso de las constelaciones,las formaciones, o clúster, es importante tener la información y desempeño de cada uno de los satélites junto con la de los objetivos a fotografiar, con lo cual se determina el uso más eficiente y minimización del tiempo de misión sobre los objetivos según sean las prioridades de misión.
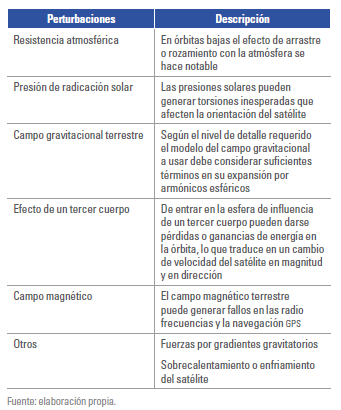
De igual modo, el segmento espacial está sometido a un sinnúmero de fenómenos identificados como perturbaciones, tal como lo muestra la tabla 3. Pese a Diseño de misión y factores o ser desconocidas, en principio, las perturbaciones en el modelamiento del sistema pueden ser estimadas y tenidas en cuenta dentro de procesos de control que permitan sobrellevar su efecto.
Tabla 3.Perturbaciones del sistema
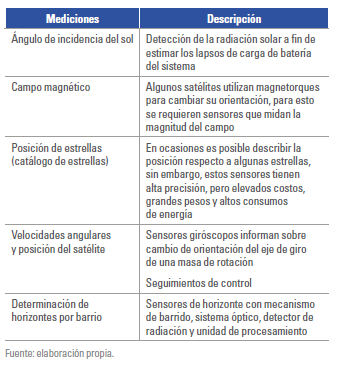
Sumado a las anteriores limitaciones y perturbaciones, algunos satélites requieren medir variables inicialmente desconocidas que influyen en la determinación de la posición relativa del satélite respecto a otros cuerpos celestes, y en el control del apuntamiento de los sensores, como se ve en la tabla 4.
Tabla 4.Mediciones operacionales de los subsistemas
Además de las limitaciones, perturbaciones y mediciones como factores básicos para la operación de los equipos satelitales, vale la pena destacar el factor relacionado con las funciones de desempeño, que depende principalmente de los bloques funcionales con los que se responde a las demandas de servicio en órbita, relacionado en el siguiente literal.
Funciones de desempeño
Como factor complementario y pauta para la deducción de las formas de representación del movimiento de los satélites de la siguiente sección, el segmento espacial puede ser representado en bloques funcionales que componen características de operación como se ilustra en la figura 3.
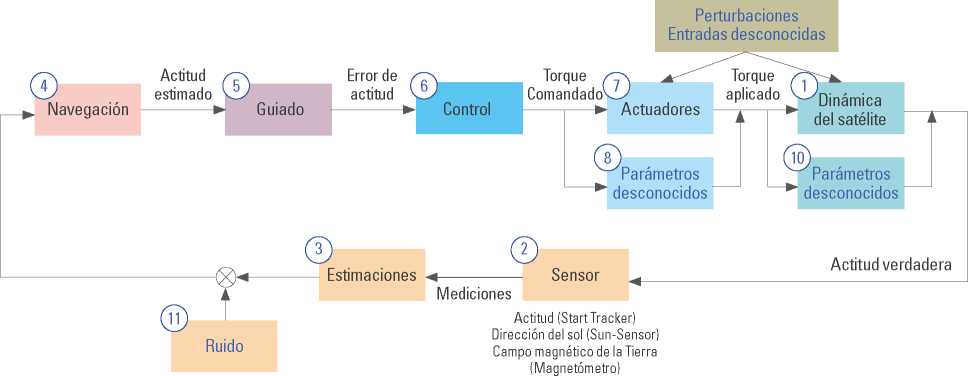 Figura 3. Bloques funcionales de un satélite genérico
Figura 3. Bloques funcionales de un satélite genérico
Fuente: Adaptado de Wertz (1978).
El primer bloque referido como la dinámica del satélite o en general la planta del sistema, tiene consigo los efectos de las perturbaciones y las dinámicas desconocidas que algunos modelos profundizan según las características funcionales y que pueden afectar la estabilidad o el control del sistema que determina su adecuada respuesta en el tiempo.
Los demás bloques representan los subsistemas de guiado, navegación, control, sensado (Sensores de sol, IMU, GPS, star tracker o magnetómetros) y medios de actuación con los que cuente el satélite (ruedas de reacción, magnetorques o propulsores), los cuales pueden ser incluidos o no en la dinámica del satélite según sea el nivel de profundidad, realismo o viabilidad conceptual que se le pueda imprimir al modelo del sistema.
Habiendo ilustrado las funciones de desempeño del segmento espacial mediante los bloques funcionales, se da paso entonces a la descripción de representaciones con las que pueden ser sintetizados los movimientos de orientación y de traslación de un satélite de acuerdo con los factores, bloques y variables previamente planteados para la comprensión del desempeño del segmento espacial.
Representaciones del segmento espacial
Como se vio en la sección anterior existe un sinnúmero de condiciones físico-matemáticas que pueden aumentar o disminuir el grado de dificultad con el que se abordan los subsistemas y bloques funcionales del satélite y, por consiguiente, los pasos del proceso de diseño de misión que los caracterizan y soportan para el proyecto espacial. Con el fin de profundizar en las herramientas disponibles para el análisis de caracterización, evaluación y definición de requisitos del segmento espacial, a continuación se muestran varios aspectos como los sistemas de referencia y representaciones de movimiento rotacional y orbital que viabilizan la composición de los subsistemas y el desempeño de los equipos satelitales dispuestos en el segmento espacial.
A. Sistemas de referencia
Sistema de referencia inercial - Inertial Frame (IF)
También conocido como J2000, la media de J2000.0. Este sistema de coordenadas ilustrado en la figura 4, describe el sistema de referencia fijado en la Tierra inercial con fecha: 01/01/2000 12:00:00 hora local de Greenwich:
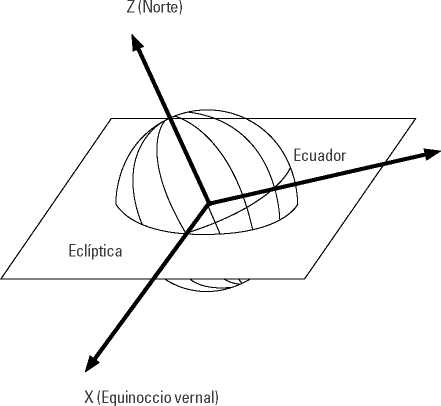 Figura 4. Sistema de referencia inercial
Figura 4. Sistema de referencia inercial
Fuente: adaptado de Sidi (1997).
- x J2000 está a lo largo del promedio del equinoccio vernal en la fecha anterior (considerando la nutación).
- z_J2000 es el eje de rotación promedio de la Tierra.
- y_J2000 completa la regla de la derecha y el plano xy es el plano promedio de Ecuador en la fecha indicada.
Sistema de referencia orbital - Orbit Frame (OF)
Este sistema de referencia se mueve con el satélite y sus ejes se definen de la siguiente manera (el plano x_OF - z_OF es el plano de órbita instantánea) según la figura 5.
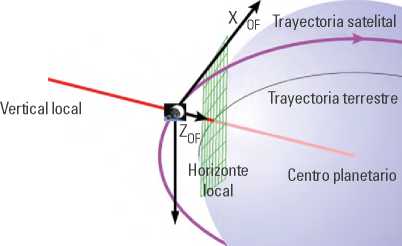 Figura 5. Sistema de referencia orbital
Figura 5. Sistema de referencia orbital
Fuente: Adaptado de Sidi (1997).
- x_OF apuntando en la dirección de la velocidad de la órbita del satélite.
- z_OF apunta en la dirección del nadir de la órbita.
- y_OF completa la regla de la mano derecha.
El nadir es la dirección desde el satélite perpendicular al plano tangente local de la cara de la Tierra. Para la Tierra redonda apunta al centro, se toma esta definición.
Sistema de referencia del cuerpo - Body Frame (BF)
Este sistema de referencia tiene su centro de coordenadas en el centro de masa del satélite, como lo muestra la figura 6; está siendo definido por el equipo de ingenieros de la misión, y varía de una misión a otra. Este sistema de referencia gira con respecto al BF por los ángulos de Euler. Una opción puede ser tomar la condición inicial de rotación donde los ángulos de Euler son cero, en este caso la RF:
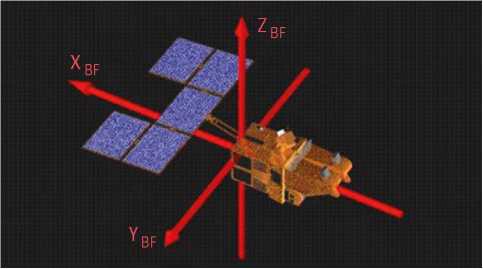 Figura 6. Sistema de referencia del cuerpo
Figura 6. Sistema de referencia del cuerpo
Fuente: Adaptado de Sidi (1997).
- x_BF apuntando en la dirección de la velocidad de la órbita del satélite.
- z_BF apunta en la dirección del nadir de la órbita.
- y_BF completa la regla de la mano derecha.
B. Representaciones movimiento de orientación o rotacional
En referencia a las formas de descripción o representación de la orientación del segmento espacial como cuerpo rígido, se tienen opciones como la matriz de cosenos directores (DCM) o matriz de rotación, ángulos de Euler, parámetros de rotación principales, cuaterniones, parámetros clásicos de Rodrigues, parámetros modificados de Rodrigues o el concepto moderno de parámetros de orientación estereográfica (Schaub & Junkins, 2009). Entre estos conjuntos se pueden tener adiciones o restas para definir el movimiento relativo, integración numérica para predecir la orientación en el tiempo, o la derivación para determinar propiedades del cuerpo rígido en representación (Younes & Mortari, 2019).
A continuación se presentan los ángulos de Euler y los cuaterniones como base para las rotaciones y movimientos relativos en el espacio.
a. Ángulos de Euler
Los ángulos de Euler son un conjunto de tres coordenadas angulares con las que se representa la orientación de un sistema de referencia de ejes ortogonales (Doroshin, 2018), como lo muestra la figura 7, generalmente móvil, respecto a otro sistema de referencia de ejes ortogonales normalmente fijos.
 Figura 7. Rotaciones en ejes fijos y móviles
Figura 7. Rotaciones en ejes fijos y móviles
Fuente: Cortés-García (2019).
De acuerdo a la figura, se realizan rotaciones alrededor de los ejes principales (sistema móvil) mediante post-multiplicaciones. Con el uso de los ángulos α, β y y se define la orientación en ángulos de Euler. Relacionando estos ángulos con los ejes x, y y z y con los números 1, 2, 3 respectivamente, se realizan unas secuencias básicas para cada rotación (Schaub & Junkins, 2009).
- Secuencia I: sin repeticiones de ejes (123).
- Secuencia II: con repeticiones de ejes (131).
De acuerdo a los procesos de secuencia, se generan 12 rotaciones para el sistema de ángulos fijos e igual número de rotaciones para un sistema de ángulos móviles, como lo ilustra la figura 8. Las rotaciones para los ángulos de Euler resultantes, son: 123, 132, 213, 231, 312, 321, 121, 131, 212, 313, y 323 (Cortés-García, 2019).
 Figura 8. Rotaciones sucesivas en ángulos de Euler
Figura 8. Rotaciones sucesivas en ángulos de Euler
Fuente: EasySpin (2014).
Es importante considerar que la secuencia 123 del sistema fijo corresponde a la secuencia 321 en el sistema móvil, con lo cual se desarrollan las siguientes ecuaciones respecto a la deducción del modelo no lineal y lineal de un satélite el cual puede ser consultado en Schaub y Junkins (2009).
• No lineal: dadas las ecuaciones dinámicas de un cuerpo fijo alrededor de un punto fijo:
• Lineal: el proceso de linealización conduce a las ecuaciones
Cuaterniones
Este modelo es la representación más utilizada actualmente para identificar el comportamiento de un satélite en órbita (Yang, 2012), además de los ángulos de Euler que por sus singularidades pasa a un segundo plano en su empleo. En este ejemplo se aplican entradas de fuerza y momentos que interactúan con el sistema (Cepeda, 2010).
Las ecuaciones que rigen al modelo de cuaterniones son (Schaub & Junkins, 2009):
Con ῶ Matriz skew-symmetric de la velocidad angular. La orientación de un satélite en el marco inercial puede ser relacionado con las velocidades angulares del eje del cuerpo, a través de los ángulos de Euler o de los cuaterniones (Francisco et al., 2018), como sigue:
Representaciones movimiento orbital o traslacional
Elementos orbitales
El modelo básico mediante elementos orbitales, considera el uso de coordenadas ecuatoriales a orbitales, donde el modelo se representa mediante matrices y vectores que evidencian los cambios y transformaciones de sistemas de coordenadas, como lo muestra la figura 9. Para ello, se definen los elementos orbitales como la excentricidad (e), semieje mayor (a), ángulo de ascensión recta del nodo ascendente (Ω), inclinación del plano orbital (i), argumento del perigeo (ω) y tiempo de paso por el perigeo perigeo (tp) (Schaub &Junkins, 2009).
 Figura 9. Sistema de coordenadas ecuatorial
Figura 9. Sistema de coordenadas ecuatorial
Fuente: Montenbruck (2005).
Para la rotación debe trabajar sobre el eje z y sobre el plano ecuatorial constituido por los ejes x, y, además del eje x para tomar las referencias, alineando con el equinoccio de primavera (Y), ya que este describe la intersección del plano ecuatorial con el plano orbital (equinoccio de primavera), determinando así la longitud y latitud requeridas. Por otro lado, en coordenadas polares, también se describen la ascensión (α), la declinación (δ) y la distancia geocéntrica (r).
La conversión entre estos dos sistemas de coordenadas es:
Con esto se pueden relacionar las coordenadas ecuatoriales a los elementos orbitales, como se ilustra en la figura 10, inclinación, recta de ascenso o nodo de ascenso RAAM (Ω) y argumento del perigeo (ω), el sistema de coordenadas de un satélite, se toma en referencia al plano ecuatorial descrito por la Tierra, y el plano orbital descrito por el satélite.
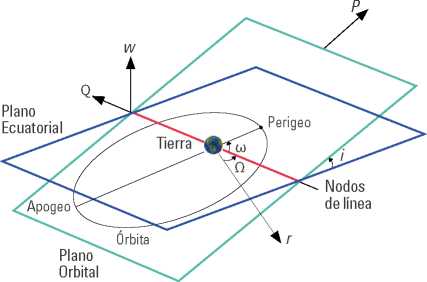 Figura 10. Elementos orbitales
Figura 10. Elementos orbitales
Fuente: Montenbruck (2005).
Los elementos orbitales enunciados y representados anteriormente, permiten la parametrización de la posición y la velocidad de los satélites, estableciendo un punto de vista físico del movimiento como un cuerpo en el espacio. En este sentido los elementos orbitales se pueden considerar como se relaciona en la tabla 5, a continuación:
Tabla 5.Descripción elementos orbitales
Los tres vectores relacionados a continuación llamados gaussianos (Schaub & Junkins, 2009) permiten definir en términos de elementos orbitales la orientación de la órbita del satélite en el espacio, de tal manera que una vez enunciados los vectores se puede determinar con claridad el cálculo de (i), (Ω), (ω) (Lin & Yan-rong, 2006).
Teniendo W como el vector perpendicular al plano de la órbita; P vector en el plano de la órbita y en el sentido del perigeo y Q el vector en el plano de la órbita y perpendicular a P, se busca que los ejes de coordenadas rectangulares coincidan con las direcciones de estos tres vectores.
Lo anterior mediante el uso de una matriz de cambio (M) conformada por matrices de giro a cada uno de los vectores, para obtener el resultado en la base X, Y, Z, de la siguiente manera:
La formulación de estos elementos orbitales puede ser aplicada a la composición de varios satélites, utilizando la diferencia de los mismos para la definición de órbita requerida, esto dispone de tres maneras, tanto para órbitas con excentricidad pequeña, como para órbitas casi circulares y movimientos limitados (Chávez, 2012).
Ecuaciones de Hill-Clohessy-Wiltshire (HCW)
En este conjunto de ecuaciones se representa el movimiento relativo de un agente respecto a un sistema de referencia LVLH (Local Vertical, Local Horizontal), centrado en el blanco y definido de forma tal que el vector unitario x tiene la dirección de R, como se muestra en la figura 11, y la dirección de la velocidad (tangente a la trayectoria), y z completa el triedro.
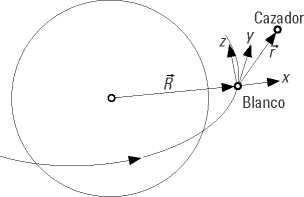 Figura 11. Sistema de referencia B-S
Figura 11. Sistema de referencia B-S
Fuente: Vázquez (2015).
En las ecuaciones se considera que el agente blanco se mueve a través de una órbita circular de radio R0, sin considerar perturbaciones orbitales y que el siguiente agente se encuentra “cerca” (1 kilómetro aproximadamente) del blanco (Sanchez & Alonso, 2010).
Estas ecuaciones presentan ventajas ya que describen el movimiento relativo a través de un sistema de ecuaciones lineales, que fácilmente pueden ser utilizadas en un sistema de control (Vassar & Sherwood, 1983).
En estas ecuaciones ω0 se escribe como sigue y 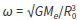 fi son las componentes de las fuerzas que estén actuando sobre el cuerpo, escritas en el marco del blanco. Si se conocen las fuerzas desde el marco inercial fijo en la Tierra, como suele suceder, es posible hacer una transformación de estas haciendo el producto con la matriz siguiente:
fi son las componentes de las fuerzas que estén actuando sobre el cuerpo, escritas en el marco del blanco. Si se conocen las fuerzas desde el marco inercial fijo en la Tierra, como suele suceder, es posible hacer una transformación de estas haciendo el producto con la matriz siguiente:
Las ecuaciones de C-W y las ecuaciones de Hill han sido utilizadas para el análisis y control de una red de satélites en Vassar & Sherwood (1983). Donde se analiza un par de satélites monolíticos en órbita, referenciando la posición de un esclavo con respecto a un maestro, y se aplica un sistema de controladores partiendo de la premisa de contar con un modelo totalmente conocido y con todos sus estados medidos.
Otro método para la representación de los sistemas en órbita es planteado en Leomanni et al. (2017), donde los elementos orbitales son los parámetros específicos con los que se modelan los cuerpos en órbita y se definen los controladores para el seguimiento de formaciones con las estimaciones cualitativas de robustez características del sistema.
De manera complementaria y con otro enfoque, la determinación de órbitas relativas puede ser determinada mediante dos métodos como el filtro de Kalman Extendido (EKF) con la ecuación dinámica relativa y la ecuación de observación del sistema o el método de mínimos cuadrados con la ecuación de estado no lineal y la ecuación de observación (Min et al., 2010), siendo estos utilizados para la formulación de una arquitectura GNC (Mooij & Ellenbroek, 2007) aplicada a una formación de satélites en vuelo (Roscoe et al., 2018).
En términos generales el recuento de representaciones se proyecta como la base teórica necesaria para la interpretación y desempeño de un satélite o varios en red con los que una misión puede ser estructurada. Habiendo considerado entonces tanto el proceso de diseño de misión como los factores operacionales y las formas de representación, se tienen los argumentos necesarios para abordar dos aplicaciones actuales, del orden nacional e internacional.
La primera refiere al ejemplo para el proceso de diseño de misión y composición de factores operacionales representada en un programa espacial de orden nacional, y el segundo, refiere la representación del segmento espacial con el concepto de Vuelo de Formación Electromagnética, que recientemente ha sido formulado como una estrategia de propulsión de gran duración para el desplazamiento de vehículos satelitales en órbita, con el que se ilustra tanto la representación del movimiento traslacional de un satélite como de un sistema de dos equipos expuestos a campos magnéticos entre sí con bobinas específicas como sistemas de actuación, con las que ajustan sus posiciones frente a fuerzas gravitacionales y perturbaciones adicionales que pueden afrontar estos equipos en el espacio.
Aplicaciones del proceso de diseño y representación del segmento espacial
Esta sección de aplicaciones retoma los resultados de las síntesis desarrolladas de las secciones I y II, con el fin de destacar la importancia no solo de seguir y estructurar un diseño de misión de un programa espacial, sino de poder interpretar y representar el segmento espacial con el que se espera cumplir las misiones para el servicio aeroespacial requerido. Se presentan dos análisis a modo de ejemplo, con los que se ilustran los conceptos de configuración de una misión, en el ejemplo 1, y el concepto de representación del movimiento del segmento espacial con una alternativa en el diseño de sistemas de propulsión como los campos magnéticos, en el ejemplo 2.
Ejemplo 1
Diseño de misión, paso 1. Programa espacial
Como ejemplo parcial del diseño de misión, a continuación se dejan planteadas las iniciativas formuladas por el Programa Espacial de la Fuerza Aérea Colombiana (FACSAT), mediante la descripción del primer paso de definición de objetivos y estimación de necesidades básicas proyectadas.
Definición de objetivos
El programa espacial FACSAT se compone de tres iniciativas o misiones para la puesta en operación de servicios de observación terrestre y una fase adicional de servicios mixtos. Las dos primeras misiones o proyectos espaciales propiamente dichos FACSAT 1 y 2, se configuran como (A) sistemas Individuales, con servicios aeroespaciales prestados por un solo agente en órbita y una sola carga útil disponible y el tercer proyecto espacial, FACSAT 3 (B) sistema multiagente (SMA1-2) configurados con más de un satélite en órbita, homogéneos o heterogéneos en red y con diferentes cargas útiles como equipos multi o hiperespectrales o equipos SAR.
A continuación se muestran los objetivos generales de las misiones y el estado de estas.
Sistema satelital individual
- FACSAT 1
- FACSAT 2
- Estado actual:
- - Fase I. Estructuración para la transferencia y diseño preliminar (en curso).
- - Fase II. Diseño conceptual y detallado y ait (fabricación, integración y pruebas Tierra).
- - Fase III. Servicio de lanzamiento / Producción académica. Véase tabla 6, numeral 2.
Objetivo: prestar servicios de observación terrestre con un satélite tipo CubeSat 3U (30x10x10cm) 4kg, para fines de iniciación y fomento del tema espacial colombiano. Se hace énfasis en procesos de investigación y desarrollo de capacidades como la estación terrera para el soporte a la operación y mantenimiento del servicio, incluso análisis en el diseño de órbita como lo muestra (Poveda, 2017).
Estado actual: operativo como lo muestra la figura 12 con su conjunto de elementos de dos líneas (TLE) y la figura 13, con el registro de una imagen de prueba, se encuentra en órbita desde el 28 de noviembre del 2018, a cargo del Centro de Investigación en Tecnologías Aeroespaciales (CITAE). Véase tabla 6, numeral 1.
 Figura 12. FACSAT1-(Two Line Element -TLE)
Figura 12. FACSAT1-(Two Line Element -TLE)
Fuente: Celestrak (s.f.).
 Figura 13. Imagen de prueba - FACSAT1 en órbita
Figura 13. Imagen de prueba - FACSAT1 en órbita
Fuente: Centro de Investigación en Tecnologías Aeroespaciales (CITAE).
Objetivo: prestar servicios de observación terrestre con mayores capacidades al FACSAT1 con un satélite tipo CubeSat 6U (30x20x10cm) 10kg, que permita la transferencia y apropiación de conocimiento para la integración del equipo, laboratorios y operación autónoma por parte del CITAE.
B. Sistema satelital multiagente
-
-Misión SMA1 - Constelación homogénea o híbrida.
- FACSAT 3
Objetivo: prestar servicios de observación terrestre y comunicaciones. Toma de imágenes en modo mosaico para cubrimiento de área mediante configuración tipo constelación con sensores ópticos o Radares de Apertura Sintética (SAR). Véase tabla 6, numeral 3.
Estado actual: proyecto multisectorial en proceso de generación de alianzas y acuerdos de servicio para su formulación y desarrollo. Esta misión tiene dos conceptos, uno académico con equipos del estándar CubeSat y otro operativo, que según las capacidades puede necesitar equipos más grandes por las características de resolución y tiempos de revisita requeridos para la toma de imágenes.
-
-Misión SMA2 - Clúster homogéneo o híbrido en formaciones.
Objetivo: prestar servicios de observación terrestre, comunicaciones, telecomunicaciones o Internet de las cosas (IoT). Útil para la toma de imágenes tipo multi-objetivo de alta precisión de apuntamiento, con sistemas híbridos de equipos multi o hiperespectrales y SAR (Ej. Misión Tándem-ESA), para el trabajo de interferometría (In-SAR o D-SAR) y modelos de elevación en 3D con control de formación y cambios de líder.
Estado actual: en proceso de investigación, con ejemplos como el análisis de arquitecturas de control y sistemas en red (Rodríguez-Pirateque & Sofrony, 2018).
Adicional al planteamiento de objetivos, a continuación se detalla parte de los requisitos cuantitativos que sustentan las misiones y con los que se formaliza la aplicación de la nueva generación de equipos en la democratización del espacio, como los nanosatélites así:
Tabla 6.Misiones del programa espacial FACSAT
Una vez definidos los objetivos generales de las misiones, se puede complementar el proceso de definición de requisitos cuantitativos de la Misión SMA1, mediante el uso del método de diseño por topología Walker Delta (Fugmann & Klinkner, 2020), para estimar el número de satélites requeridos a partir de relaciones geométricas como lo ilustra la figura 14, aunque con unas variaciones donde se considera un solo plano orbital desde el inicio del tratamiento geométrico (Mingqi et al., 2017) y se realizan las siguientes suposiciones:
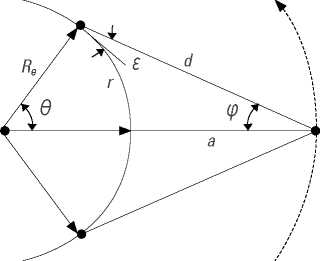 Figura 14. Relación trigonométrica entre los distintos elementos del método Walker
Figura 14. Relación trigonométrica entre los distintos elementos del método Walker
Fuente: Prescornitoiu & Morales (2019).
- Misión SMA1
• Tipo de órbita: LEO
• Altitud (a): 500-700 km
• Un solo plano orbital
• Ángulo de elevación mínima(s) 10 grados
El método utiliza las siguientes ecuaciones junto a los valores anteriores para calcular el radio de cobertura:
A partir de este valor se calcula el ángulo de cobertura:
Y con este se calcula el radio de cobertura como una longitud de arco terrestre:
Considerando que los satélites se solapan, se asume el área de cobertura de cada satélite como el de un hexágono. Para el cálculo del área total de interés se asume que es el producto del perímetro de la Tierra por un ancho hipotético dado como la distancia máxima entre los extremos norte y sur de Colombia, est es, aproximadamente, 1800 km para un área total de cobertura de 72*103km2
El método entrega los siguientes valores:
- Área de cobertura individual: 6.351.823 - 9.803.330,84 km2
- Radio de cobertura: 1.563,59 - 1.942,5 km
- Número estimado de satélites: 17 en un solo plano orbital a 500 km de altura
El método anterior sirve como primera aproximación y ejemplo para la estimación del número de satélites, sin embargo, es posible que considere un número de satélites y planos orbitales con los cuales la viabilidad de la misión puede estar fuera de alcance.
En este sentido, el programa espacial está abierto a recibir propuestas desde diferentes ámbitos, dentro de las cuales se destacan propuestas institucionales y comerciales para el proyecto FACSAT3, una de ellas enuncia que se podría componer de tres constelaciones con 14, 4 y 2 satélites configurados con diferentes características de carga útil en diferentes planos orbitales, la segunda propuesta plantea 4 constelaciones con 8 a 12 satélites por plano y una tercera propuesta, sería con 6 satélites en una sola constelación, 4 con sensores ópticos (RGB, NIR, PAN), 1 radar de apertura sintética (SAR) y 1 hiperespectral de 180 bandas, como arquitectura mínima para las necesidades. En términos generales, pueden darse otras alternativas de diseño según las alianzas y actores involucrados o los recursos disponibles para los usuarios y servicios demandados en la política nacional formulada y, para ello, se hace necesario un análisis más detallado continuando los demás pasos del diseño.
Finalmente, la disposición particular de los sistemas multiagente tanto en la Misión SMA1 tipo constelación como la Misión SMA2 tipo clúster con formaciones específicas o demás misiones expuestas de agentes individuales, requieren ser estudiadas y evaluadas para el resto de pasos del diseño de misión. Particularmente debe entender el impacto y aporte de los factores operacionales y las formas de representación de los movimientos de orientación y de traslación, como respaldo a la caracterización de misión y definición de requisitos funcionales, operativos y restricciones que pueden componer cualquier misión.
Ejemplo 2
Representaciones del movimiento / Sistema EMFF
Este ejemplo parte de la necesidad del programa espacial expuesto en el ejemplo 1. Busca la manera de representar una misión tipo multiagente como las mencionadas en las posibles configuraciones del proyecto FACSAT3, en caso de generarse configuraciones de segmentos espaciales que requieran cambios de órbita o movimientos específicos, en caso de considerar propuestas de constelaciones o algún tipo de formación especial con cargas útiles que requieran movimientos rotacionales o traslacionales para sus resultados finales.
Evaluando a su vez el alcance y viabilidad física del sistema de actuación con campos magnéticos como alternativa de propulsión para esos tipos de configuraciones.
El modelo conocido como Electromagnetic Formation Flying (EMFF) parte de la formulación de Euler-Lagrange (véase Chung et al. (2009)) y es aplicado a redes de satélites con un número arbitrario de agentes que se atraen o se repelen con fuerzas electromagnéticas para su traslación dentro de la formación. Se considera que cada satélite cuenta con tres bobinas cuyo vector área apunta en las tres direcciones de un sistema de referencia ortogonal unido al satélite, además cada satélite cuenta con tres ruedas de reacción.
Al encender alguna, o varias bobinas, el satélite genera un campo magnético que afecta a los demás. Simultáneamente, al activar su bobinado se ve afectado por los campos generados por los otros satélites de la formación (y por el de la Tierra). Estos efectos magnéticos generan movimientos de traslación relativa entre satélites. A la par, en los agentes afectados se crean torques magnéticos no deseados que serán controlados a través de las ruedas de reacción. Las ecuaciones de movimiento más generales para este sistema, desde un marco inercial fijado en la Tierra, se escriben como sigue:
En estas se modela el efecto gravitacional de la Tierra haciendo uso de una expansión del potencial de un cuerpo real hasta el J2. En la expresión anterior Re es el radio de la Tierra, Ri la posición del satélite desde el centro de la Tierra, Fdi son las componentes de las posibles fuerzas de perturbación (presión solar, fricción atmosférica, ruido cuántico, entre otras), los valores de i, son los momentos de inercia del satélite respecto a un sistema de referencia puesto sobre sus ejes principales, los valores de Ω son las componentes de la velocidad angular de las ruedas de reacción, mientras que ω es la velocidad angular del satélite.
Los términos Tdi y Trw son los torques generados por las fuerzas de perturbación y por las ruedas de reacción, respectivamente. Por último, Fm y Tm son las fuerzas y los torques magnéticos. Dado que los campos magnéticos están siendo generados por bobinas cuyos diámetros se consideran significativamente menores a las distancias entre satélites, se aproxima el campo magnético de cada satélite por el de un dipolo. Así, se pueden escribir las fuerzas y los torques hechos por el j- ésimo satélite sobre el i- ésimo en términos del momento magnético dipolar de cada uno de estos así:
Es decir, las fuerzas y torques magnéticos que siente el i- ésimo satélite es la suma de las contribuciones de las hechas por los j- ésimos. Estas contribuciones pueden calcularse como se sigue:
Al igual que los demás modelos, los sistemas EMFF tienen limitaciones en su implementación.
Las formas funcionales de la fuerzas entre satélites, que incluyen términos que decaen con el inverso de la quinta potencia de la distancia, 1/r 5 plantean limitantes para los movimientos traslaciones de satélites que estén alejados entre sí. La figura 15 considera que cada satélite cuenta con una bobina alineada en el eje de movimiento. Ambas bobinas tienen momentos magnéticos dipolares de 1*104Cm2/s y cuentan con separaciones iniciales distintas señaladas en cada imagen. Se ignoran los efectos gravitacionales.
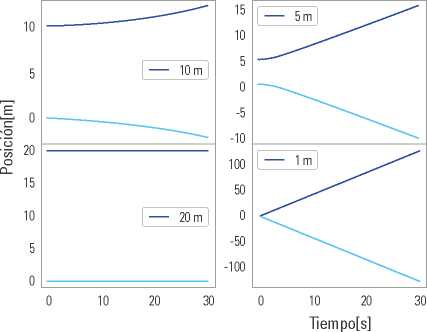 Figura 15. Movimiento de dos satélites alineados entre sí
Figura 15. Movimiento de dos satélites alineados entre sí
Fuente: elaboración propia.
En esta se observa que para dos satélites con momentos magnéticos dipolares de 104A y distancias iniciales, por ejemplo, de 10m los movimientos resultantes son de 1m en 20 segundos. Obtener momentos de este orden puede ser complejo teniendo en cuenta que el momento está dado por μ = niA, con n el número de vueltas de alambre, i la corriente y A el área. Sin embargo, se ha mostrado que para misiones de larga duración, donde los satélites se encuentren a distancias cortas, o, donde los movimientos requeridos sean de precisión las condiciones de ahorro de energía del sistema son sobresalientes.
A partir de las ecuaciones (29), que tratan la dinámica de traslación, y realizando las transformaciones necesarias con la matriz (16) es posible obtener los elementos orbitales de los satélites para tener una representación estandarizada de la posición satelital.
Por otra parte, las ecuaciones (IV-B) que describen la dinámica rotacional del satélite conllevan a la obtención del vector velocidad angular ω̇. Con este y las ecuaciones (8) se puede llegar fácilmente a los ángulos de Euler o a los cuaterniones, según se escoja. Ambas descripciones definen de manera clara la posición del cuerpo.
Por último, las ecuaciones C-W dan una descripción del movimiento de alguno de los satélites respecto al otro, en el caso de dos satélites EMFF, para este sistema las fuerzas f de la ecuación (22) son las fuerzas magnéticas (31) ocasionadas por el primer satélite sobre el segundo. Estas fuerzas deben estar escritas en el marco del primer satélite, para esto basta realizar una transformación usando la matriz (23).
A manera de ejemplo en las figuras 16 se muestran los movimientos de dos satélites EMFF en órbita LEO con sus 3 bobinas magnéticas activadas. En a, la trayectoria se muestra desde el marco de la Tierra y los ejes cuentan con escalas distintas. En b, la figura muestra el movimiento relativo del segundo satélite desde el marco de referencia del primero. Ambos satélites tienen activadas sus bobinas y parten de una separación inicial de 5 metros. Acá se aprecia la importancia de trabajar con las posiciones relativas pues los desplazamientos que son productos de las perturbaciones en las órbitas son notables.
 Figura 16. Trayectorias de satélites en órbita LEO
Figura 16. Trayectorias de satélites en órbita LEO
Fuente: elaboración propia.
Al tener todo su bobinado activado el satélite obtiene un desplazamiento de algunos metros a lo largo de este eje. Además, se aprecia la importancia de tener una configuración adecuada para la red, pues a lo largo de la órbita se crean efectos perturbativos no deseados entre un satélite y el otro producto de los efectos inerciales.
Conclusiones
El esquema general del documento permitió recopilar dentro del concepto de sistema espacial el proceso para el diseño de misión, los factores operacionales y la representación del segmento espacial. Esta recopilación es la base para la conformación de herramientas y soluciones en la articulación de diseños, inclusión de características y análisis del comportamiento del segmento, que al final formalizan los análisis de operatividad y estructuración dentro de un proyecto espacial para la apropiación de las tecnologías espaciales.
Este estudio se desarrolló con el fin de brindar herramientas de análisis y planeación para el diseño de misiones, en las que se puedan caracterizar los tipos de servicio aeroespacial, así como de reconocer los componentes físicos, los diferentes subsistemas satelitales y el análisis matemático de la operación de los satélites planteados en el diseño de misión. Herramientas que sirven como base para la operación de un satélite como único agente del sistema o para la interpretación de satélites en red como es el caso de las constelaciones, clúster, enjambres o formaciones de vuelo.
Se desarrollaron dos aplicaciones sustanciales para la consolidación de los conceptos y presentación de misiones y modelos de actuación. Una para el diseño de misión con la síntesis de objetivos del programa espacial FACSAT y otra con la aplicación y uso de los medios de representación para una simulación del concepto de vuelo de formación electromagnética de dos satélites. Con el análisis de este concepto y el desarrollo anterior se ilustró no solo la utilidad de los desarrollos previos sino que se analizó la viabilidad y alcance de dicha tecnología en operaciones de órbita baja como la observación terrestre.
Como trabajos futuros se recomienda la profundización en los demás pasos del proceso de diseño de misión para la estructuración de proyectos espaciales que impliquen sistemas de control en red, o demás necesidades de configuración para misiones de observación terrestre con sistemas segmentados.
Finalmente, de acuerdo con las simulaciones realizadas de la operación del sistema EMFF, se pueden estudiar diferentes sistemas de propulsión para los movimientos traslacionales, que puedan ser configurados de forma viable y efectiva dentro del diseño de misión.
Referencias bibliográficas
Agencia Espacial Mexicana [AEM]. (2013). Introducción a los Sistemas Espaciales. Secretaría de comunicaciones y Trasportes, SCT. http://www.educacionespacial.aem.gob. mx/images/normateca/pdf/CURSO_ISE/Modulo_3.pdf
Álvarez-Reyna, M., Pucheta, J., & Fraire, J. (2019). Determinación precisa de posición y orientación relativa en satélites de arquitectura segmentada. Ajea, (4), 4-6. https:// doi.org/10.33414/ajea.4.356.2019
Blasch, E., Pham, K., Chen, G., Wang, G., Li, C., Tian, X., & Shen, D. (2014, October 5-9). Distributed qos Awareness in Satellite Communication Network With Optimal Routing (Quasor) [Conferencia]. IEEE/AIAA 33rd Digital Avionics Systems Conference (DASC). Colorado Springs, CO, USA. https://ieeexplore.ieee.org/document/6979501
Braukhane, A., Arza, M., Bacher, M., Calaprice, M., Fiedler, H., Koehne, V., McGuire, H. R., & Rivera, J. J. (2010, marzo 6-13). FormSat, A Scalable Formation Flying Communication Satellite System [Conferencia]. IEEE Aerospace Conference. Big Sky, MT, USA. https://ieeexplore.ieee.org/ document/5446999
Burleigh, S. C., De Cola, T., Morosi, S., Jayousi, S., Cianca, E., & Fuchs, C. (2019, mayo). From Connectivity to Advanced Internet Services: A Comprehensive Review of Small Satellites Communications and Networks. Wireless Communications and Mobile Computing, (11), 1-17. https:// doi.org/10.1155/2019/6243505
Cepeda, R. (2010). Sistema de control robusto, basado en cuaterniones, para un satélite de órbita baja [Tesis de Maestría]. Pontificia Universidad Javeriana. https://repository.ja veriana.edu.co/bitstream/handle/10554/12728/Cepe daGomezRudy2010.pdf?sequence=1&isAllowed=y
Chávez, S. (2012). Diseño conceptual de un simulador de navegación aeroespacial y prototipo inicial [Tesis de Maestría]. Instituto Nacional de Astrofísica, Óptica y Electrónica. https://inaoe.repositorioinstitucional.mx/jspui/bits tream/1009/304/1/ChavezBS.pdf
Chung, S. J., Ahsun, U., & Slotine, J. J. E. (2009). Application of Synchronization to Formation Flying Spacecraft: Lagrangian Approach. Journal of Guidance, Control, and Dynamics, 32(2), 512-526. https://inaoe.repositorioinstitucional.mx/jspui/bits tream/1009/304/1/ChavezBS.pdf
Cortés-García, E. D. (2019). Experimentación del control de actitud en un prototipo de CubeSat con ruedas de reacción [Tesis de pregrado]. Universidad Nacional de Colombia. https://doi.org/10.13140/RG.2.2.24678.3744
Doroshin, A. V. (2018). Attitude Dynamics, Control and Stabilization Of Spacecraft / Satellites. Samara State Aerospace University. https://n9.cl/ihlyr
EasySpin. (2014). Rotations and Euler angles. EasySpin. https:// easyspin.org/easyspin/documentation/eulerangles.html
Francisco, A., Somma, J., Dra, D., Lorena, M., & Optar, P. (2018). Cuaterniones y ángulos de Euler para describir rotaciones en R3. Universidad abierta interamericana. http:// imgbiblio.vaneduc.edu.ar/fulltext/files/TC126683.pdf
Fugmann, M., & Klinkner, S. (2020). An Automated Constellation Design & Mission Analysis Tool for Finding the Cheapest Mission Architecture [Conferencia]. SSC20-I-07 Mission Architecture, 34th Annual Small Satellite Conference, I (07), 1-12.
Gurfil, P., Herscovitz, J., & Pariente, M. (2012). SSC12-VII-2 The Samson Project - Cluster Flight and Geolocation with Three Autonomous Nano-satellites [Conferencia]. 26 th Annual AIAA/USU Conference on Small Satellites. Utah, USA. https://www.researchgate.net/publication/272710981_ SSC12-VII-2_The_SAMSON_Project_-_Cluster_Flight_ and_Geolocation_with_Three_Autonomous_Nano-sa tellites
Larson, W. J., & Wertz, J. R. (Eds.). (1999). Space Mission Analysis and Design. United States of America (3rd ed.). Microcosm Press.
Leomanni, M., Bianchini, G., Garulli, A., & Giannitrapani, A. (2017). A Class of Globally Stabilizing Feedback Controllers for the Orbital Rendezvous Problem. International Journal of Robust and Nonlinear Control, 27(18), 46074621. https://doi.org/10.1002/rnc.3817
Lin, L., & Yan-Rong, W. (2006). An Analytical Method for Satellite Orbit Prediction. Chinese Astronomy and Astrophysics, 30(1), 68-74. https://doi.org/10.1016/j.chinastron.2006. 01.006
Marsden, R. G. (2002, julio). Basic Steps in Designing a Space Mission - A short tutorial. ESA. https://swe.ssa.esa.int/TECEES/ spweather/Alpbach2002/Marsden-basic%20steps%20 in%20designing%20a%20space%20mission.pdf
Mazal, L., & Gurfil, P. (2014). Closed-loop Distance-keeping for Long-Term Satellite Cluster Flight. Acta Astronautica, 94(1), 73-82. https://doi.org/10.1016/j.actaastro.2013. 08.002
Min, H., Guoqiang, Z., & Junling, S. (2010, octubre 22-24). Navigation and Coordination Control System for Formation Flying Satellites [Conferencia]. International Conference on Computer Application and System Modeling, ICCASM 2010. Taiyuan, China.
Mingqi, Y., Xurong, D., & Min, H. (2016, agosto 12-14). Design and Simulation for Hybrid LEO Communication and Navigation Constellation [Conferencia]. 2016 IEEE Chinese Guidance, Navigation and Control Conference, CGNCC. Nanjing, China.
Montenbruck, O. (2005). Satellite Orbits Models - Models, Methods and Applications. Berlin Heidelberg.
Mooij, E., & Ellenbroek, M. (2007, agosto 20-23). Multi-Functional Guidance, Navigation, and Control Simulation Environment [Conferencia]. AIAA Modeling and Simulation Technologies Conference and Exhibit. South Carolina, USA. https://arc.aiaa.org/doi/abs/10.2514/6.2007-6887.
NASA (2007). Systems Engineering Handbook. National Aeronautics and Space Administration, NASA Center edition.
Navarro, W. (2016). Improving Attitude Determination and Control of Resource-constrained CubeSats Using Unscented Kalman Filtering [Tesis de maestría]. Massachusetts Institute of Technology https://dspace.mit.edu/ handle/1721.1/105621
Poveda, G. A. (2017). Propuesta de órbita geoestacionaria para el satélite artificial FACSAT 01. [Tesis de maestría]. Universidad del Valle.
Prescornitoiu, B., & Morales, M. (2019). Estudio y diseño de constelaciones de nanosatélites en el marco de las comunicaciones IoT [Tesis de pregrado]. Universidad Carlos III de Madrid. https://e-archivo.uc3m.es/handle/ 10016/29810
Radhakrishnan, R., Edmonson, W. W., Afghah, F., Rodriguez-Osorio, R. M., Pinto, F., & Burleigh, S. C. (2016, mayo). Survey of Inter-Satellite Communication for Small Satellite Systems: Physical Layer to Network Layer View. IEEE Communications Surveys & Tutorials, 18(4), 2442-2473. https://doi.org/10.1109/COMST.2016.2564990
Rodríguez-Pirateque, G. W., & Sofrony Esmeral, J. (2018). Revisión de sistemas de control en red como base para sistemas satelitales de pequeña escala. Ciencia y Poder Aéreo, 13(2), 90-125. https://doi.org/10.18667/cienciay poderaereo.604
Roscoe, C. W., Westphal, J. J., & Mosleh, E. (2018). Overview and gnc Design of the CubeSat Proximity Operations Demonstration (CPOD) mission. Acta Astronautica, 153, 410-421. https://doi.org/10.1016/j.actaastro.2018.03.033
Sánchez, R., & Alonso, R. (2010). Control de Vehículos Espaciales. Revista Iberoamericana de Automática e Informática Industrial, 2(3), 6-24. http://hdl.handle.net/102 51/146465
Schaub, H., & Junkins, J. (2009). Analytical Mechanics of Space Systems (2nd ed.). American Institute of Aeronautics & Astronautic, AIAA.
Sidi, M. J. (1997). Spacecraft dynamics and control - A practical engineering approach. Israel Aircraft Industries Ltd. and Tel Aviv University.
Vassar, R. H., & Sherwood, R. B. (1985, marzo). Formation Keeping for a Pair of Satellites in a Circular Obit. Journal of Guidance, Control, and Dynamics, JGCD, 8(2). https://arc. aiaa.org/doi/10.2514/3.19965
Vázquez, R. V. (2015). Mecánica Orbital y Vehículos Espaciales. Universidad de Sevilla.
Wertz, J. (1978). Spacecraft Attitude Determination and Control. Springer Science & Business Media.
Xu, S., Wang, X.W., & Huang, M. (2018, enero). Software-Defined Next-Generation Satellite Networks: Architecture, Challenges, and Solutions. IEEE Access, 6, 4027-4041. https://doi.org/10.1109/ACCESS.2018.2793237
Yang, Y. (2012, December). Spacecraft Attitude Determination and Control: Quaternion based method. Annual Reviews in Control, 36(2), 198-219. https://doi.org/10.1016/j. arcontrol.2012.09.003
Younes, A. B., & Mortari, D. (2019). Derivation of All Attitude Error Governing Equations for Attitude Filtering and Control. Sensors, 19(21), 4-6. https://doi.org/10.3390/s192 14682