http://dx.doi.org/10.18667/cienciaypoderaereo.493

Artículo
CIENCIA Y PODER AÉREO 11(1): 176-185, 2016

Análisis de tolerancia al daño bajo el criterio de fractura elástico-lineal del ala de una Aeronave Categoría Deportiva (LSA)¹

Analise de tolerância ao dano sob o criterio de fratura elástico-lineal da asa de uma Aeronave de Categoria Esportiva (LSA)²

Analysis Of The Damage Tolerance Under The Criterion Of The Elastic-Linear Fracture Of The Wing Of A Sports Category Aircraft (LSA)³

Fabio Alejandro Merchán Rincón⁴, Andrés Alberto Ayala Flórez⁵, Christian Fabián Rodríguez⁶,
Fernando Alberto Quintero Vargas⁷
Universidad San Buenaventura

Recibido: 15/06/2016
Aprobado evaluador interno: 30/07/2016
Aprobado evaluador externo: 25/08/2016

Para citar este artículo:
Merchán, R, Ayala, A., Rodríguez, C, & Quintero, F. (2016). Análisis de tolerancia al daño bajo el criterio de fractura elástico-lineal del ala de una aeronave categoría deportiva (LSA). Ciencia y Poder Aéreo, 11 (1), 176-185. Doi: http://dx.doi.org/10.18667/cienciaypoderaereo.493

Resumen: el siguiente artículo presenta una metodología de aplicación de un análisis de tolerancia al daño en la estructura del ala de una aeronave categoría LSA. Este estudio contempla un análisis CFD en ANSYS Fluent donde se calculan las cargas aerodinámicas que actúan sobre el ala, seguido de un análisis de resistencia estructural en el cual se realiza una Integración Fluld-Structure Interface con la que se determinan los esfuerzos máximos soportados por la estructura mediante Elementos Finitos (FEA) realizado en ANSYS Workbench, un análisis de tamaños de grieta críticos, sobre los elementos primarlos de la estructura y un cálculo de vida residual de estos elementos con el fin de crear un Intervalo de Inspecciones NDT para garantizar la integridad estructural del ala de la aeronave.

Resumo: o artigo a seguir apresenta uma metodologia de aplicação de um analise de tolerância ao dano à estrutura da asa duma aeronave categoria LSA. Esse estudo contém um analise CFD em ANSYS Fluent onde são calculadas as cargas aerodinâmicas que agem sobre a asa seguido dum analise de resistência estrutural no qual e feita uma integração Fluid-Structure Interface com a qual são determinados os esforços máximos suportados pela estrutura por melo de Elementos Finitos (FEA) realizado em ANSYS Workbench, um analise de tamanhos de fenda críticos sobre os elementos primários da estrutura e um calculo de vida residual destes elementos com a finalidade de criar um intervalo de inspeções NDT para garantir a integridade estrutural da asa da aeronave.

Abstract: The following article presents a methodology for applying a Damage Tolerance Analysis to the wing structure of an LSA category aircraft. This study contemplates a CFD analysis in ANSYS Fluent where aerodynamic loads that work on the wing are calculated, followed by a structural reslstance analysls In whlch an Integratlon Fluld-Structure Interface Is made to determine the máximum stresses supported by the structure uslng Flnlte Element (FEA) performed in ANSYS Workbench, an analysis of critical crack sizes on the primary elements of the structure and a residual life calculation of this elements in order to create NDT inspections intervals to ensure structural integrity of the aircraft wing.

Nomenclatura

λ = Relación de taperado (C/C)

β = Factor concentrador de grieta

σ = Esfuerzo soportado por la pieza

ΔN = Número de ciclos para falla de la pieza

a = Tamaño de la grieta

acrit = Tamaño crítico de grieta

af= Tamaño final de la grieta

ai = Tamaño inicial de la grieta

AR= Relación de aspecto del ala

b = Envergadura del ala

C_D = Coeficiente de arrastre aerodinámico

C_D0 = Coeficiente de arrastre parásito

C_r = Cuerda en la raíz del ala

C_t = Cuerda en la punta del ala

C_t = Coeficiente de sustentación

D = Diámetro del agujero

e = Eficiencia de Oswald

Kc = Factor de intensidad de esfuerzo

L = Fuerza de sustentación

Le = Fuerza de sustentación ideal para un ala elíptica

Lt = Fuerza de sustentación ideal para un ala taperada

n= Factor de carga

Nr= Número de ciclos para inspección segura

SF = Factor de seguridad

W = Ancho de la pieza

W_MTOW = Peso máximo al despegue

y = posición a lo largo de la envergadura (eje y)

Abreviaturas y definiciones

CAD ComputerAided Design - Diseño asistido por computadora.

CFD Computer Fluid Dynamics - Dinámica de fluidos computacional.

FSIFluid-StructureInterface-Interacción Fluido-Estructura. Flomebullt Aeronave hecha en casa.

LSA Light SportAircraft - Aeronave deportiva ligera. MFFL Mecánica de Fractura Elástico-Lineal.

NDFNon-Destructlve Festlng - Ensayos no destructivos. Twist aerodinámico Diferencia entre los perfiles aerodinámicos de la raíz y la punta del ala.

Twist geométrico Diferencia entre el ángulo que conforma la cuerda de la raíz y la punta del

ala respecto a la dirección del viento.

QuadTipo de elemento empleado en CFD cuya característica principal es su

forma rectangular en 2D o prismática en 3D.

Introducción

Las aeronaves LSA son ampliamente usadas en la aviación civil, algunas de estas aeronaves no poseen certificación tipo, por dicha condición el desgaste y fatiga por el ciclaje no han sido calculados de una manera rigurosa en la estructura del ala; para este estudio se utilizó como ejemplo una aeronave homebuilt de dos pasajeros, de ala baja en voladizo, totalmente fabricada en aluminio. Dicha aeronave ha presentado en el pasado una serie de accidentes que llevó a los entes reguladores de la aviación civil a pensar que el diseño del ala no era seguro, debido a esto es necesario la implementación de un análisis de tolerancia al daño, para determinar de manera analítica los intervalos de inspección para su uso seguro.

El análisis de tolerancia al daño se realizó, en primer lugar, determinando las cargas a las cuales está sometida la aeronave en condiciones críticas de vuelo mediante un análisis CFD, validado de manera analítica, después por medio del programa de elementos finitos ANSYS en su módulo Workbench se calcularon los esfuerzos causados por las cargas que soporta el ala, se determinaron los elementos críticos, aquellos que soportan mayores esfuerzos y que poseen un menor factor de seguridad; para dichos elementos se estimó un tamaño crítico de grieta, si la grieta alcanza dicho tamaño la pieza fallará, y por último se determinaron los tiempos de inspección seguros para que dichas grietas no se presenten. Los métodos de inspección usados para este análisis fueron: Ultrasonido, Corrientes de Eddy e inspección visual por medio de Boroscopio, los tiempos de inspección para cada uno de los NDTs usados varían por la precisión de las inspecciones al detectar grietas en el material.

Estimación de cargas y esfuerzos

Estudio de cargas aplicadas por medio de CFD

El estudio comienza con la superficie del ala modelada en software CAD, la cual es importada en el modelador de ANSYS y se genera sobre ésta un encerramiento que será el dominio donde se analizará el fluido, y servirá para asignar las condiciones de frontera del análisis, en este caso una entrada de aire a una velocidad de 54m/s que corresponde a la velocidad de maniobra de la aeronave a nivel del mar, con un número de Reynolds de 4,5E+6 que significa un régimen turbulento de operación, para el cual se selecciona el método de turbulencia Spalart-Allmaras, las paredes laterales del dominio se asignan como non slip waiis, por último se asigna un outletpressure como salida del fluido.

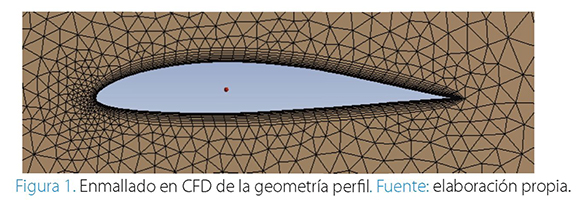
Se enmalla el dominio del fluido con elementos tetraédricos (Figura 1), se realiza un refinamiento en la cercanía de la superficie del ala y se realiza un enmallado híbrido sobre la superficie que conforma el ala, estructurado por elementos prismáticos con un aumento progresivo de su tamaño, esto con el fin de captar mejor el comportamiento de la capa límite del perfil y así mismo obtener mejores resultados de las fuerzas sobre la geometría.

Se programan monitores para obtener la fuerza total de sustentación y de arrastre aerodinámico al final de la simulación para los cuales corresponde 3084,22 [N] y 221,041 [N] respectivamente, en este punto es posible graficar los resultados de la presión estática sobre el ala, los cuales se muestran en la Figura 2.

Se emplea el método 5cfiren/c(Schrenk, 1940) para determinar la distribución de las cargas aerodinámicas sobre el ala (figura 3) y de esta forma validar el análisis por CFD, este método seml-empírlco asume que para un ala de relación de aspecto finita, con bajo o nulo flechamlento, sin twist aerodinámico o geométrico y bajo una condición de operación donde el aire se considera Incompresible, existe una variación en la distribución de sustentación, ésta distribución depende de la forma del ala, donde se relaciona un ala elíptica (cuya distribución de carga es ideal, denotada como Le) y un ala taperada, para este caso (donde su distribución de carga es lineal variando únicamente la cuerda del perfil a lo largo de la envergadura, denotada como Lt), por último los resultados de las dos distribuciones asumidas son promediados para obtener una aproximación final, que se asemeja al comportamiento real de la sustentación sobre el ala.

Para hallar la distribución del arrastre aerodinámico (Figura 4) también se emplea el método Schrenk, con la diferencia que se debe calcular el arrastre total para así obtener la distribución sobre el ala. El arrastre consiste en la suma de las contribuciones del arrastre parásito, Inherente a la forma y a la superficie expuesta al fluido, y el arrastre Inducido, debido a la eficiencia aerodinámica del ala, estos valores se expresan en coeficientes.

De esta manera se puede realizar el producto entre el coeficiente de arrastre y las condiciones de vuelo de la aeronave para determinar el arrastre total.

Se procede con la comparación de ambos análisis para ello se emplea la ecuación (5) donde se determina la diferencia porcentual o el “error” entre los valores obtenidos donde se tiene finalmente que, para la fuerza de sustentación total, obtenida del análisis CFD y de la integración del área bajo la curva de la distribución de sustentación lograda analíticamente, la diferencia porcentual es igual a 4,89% lo cual está dentro del valor aceptable de error. Para los valores de arrastre aerodinámico la diferencia porcentual es de 9,14%, este valor es alto en cierta medida; esto se debe principalmente al dispositivo en la punta del ala, el wing-tip tipo hoerner que ayuda a una mejor transición de los vórtices en la punta del ala, disminuyendo el c/rag total y mejorando la eficiencia aerodinámica, esto no se consideró en el cálculo analítico y de allí la alta diferencia entre los valores.

Análisis de esfuerzos en ANSYS Workbench

A partir de los planos originales de la aeronave se crea un modelo simplificado en software CAD, como se observa en la Figura 5 (Catia V5), este modelo idealiza cada uno de los componentes de la estructura del ala como superficies, esto disminuye considerablemente la cantidad de nodos y elementos necesarios en el enmallado, conservando la precisión en los resultados posteriormente.

El preprocesamiento del modelo en ANSYS consiste en nombrar las secciones del modelo para una mayor facilidad en su manejo, se realizan las conexiones pertinentes entre cada una de las superficies asemejándolas a las uniones de la estructura real y se asigna un espesor a cada una de las partes. Los materiales utilizados para la simulación son el AI2024-T3 y Al 6061-T6 (ASM Aerospace Specifica-tion Materials Inc., 2016), estas son algunas de las aleaciones de aluminio más utilizadas en la industria aeronáutica.

Se utiliza una malla tipo Quad (Figura 6), ampliamente utilizado en análisis estructural debido a que este tipo de malla estructurada se acopla mejor a cada una de las superficies de la geometría simplificada, el uso de una malla con elementos triangulares podría inducir concentradores de esfuerzos, lo que provocaría errores en los resultados. Adicionalmente, se tiene en cuenta que el tamaño de elemento sea el suficiente para garantizar cierta precisión en el análisis, esto se hace mediante una convergencia de malla, donde se realiza un proceso iterativo donde la variable es el tamaño de los elementos de la malla, todas las pruebas están sometidas bajo las mismas condiciones de carga, y se cambia progresivamente la densidad de la malla hasta obtener una tendencia en los valores de esfuerzo, obtenidos en cada iteración. Finalmente, se restringe el modelo limitando los grados de libertad en la raiz del ala, asemejando una estructura en voladizo, luego se realiza la importación de la distribución de presiones desde CFD para ser aplicada sobre la estructura (Figura 7), a esto se le llama Fluid-StructureInterface (FSI) (ANSYS, Inc., 2011).

Se puede observar la deformación total del ala, según Figura 8, bajo las cargas aerodinámicas máximas (factor de carga 4 determinado por la envolvente de vuelo) donde el mayor valor de deformación es de 1,568in en la punta del ala con Aluminio 2024-T3 y de 1,663in con Aluminio 6061-T6.

En la Figura 9, se puede observar el comportamiento de los esfuerzos normales a lo largo de la viga principal de la estructura, se aprecia que el ala se encuentra bajo flexión, donde la parte inferior está sometida a tensión, condición bajo la cual es probable la generación de grietas. El esfuerzo máximo a tensión se encuentra en la viga trasera, punto donde el factor de seguridad mínimo para el aluminio 2024-T3 es de 1,2, con la aleación 6061-T6 es de 1,07, estos valores son muy bajos (Una estructura certificada por la FAR 23 debe tener como mínimo un FS de 1,5 (Federal Aviation Administration, 23.303. Amdt. 62), lo que supone un margen de seguridad muy cerrado para que la estructura soporte factores de carga mayores a 4, adicionalmente es más susceptible a una falla por fatiga.

Análisis de tolerancia al daño

Tamaño de grieta crítica y tiempos de inspección

Este análisis se realizó utilizando la teoría de Mecánica de fractura lineal elástica como modelo de crecimiento de grieta, para este análisis se tuvieron en cuenta tres tipos de grietas, grieta de borde, grieta de agujero con crecimiento simétrico y grieta de agujero con crecimiento asimétrico como se puede ver en la Figura 10.

Adicional, es importante tener buen criterio para definir el tipo de grieta que se puede llegar a presentar en la estructura, ya que no todas tienen el mismo tipo de falla. Esto depende de las condiciones geométricas y de uso del componente. En este estudio, el tipo de grieta que más afecta los componentes del ala es la grieta asimétrica en agujero, debido a la distribución de esfuerzos y a los agujeros de remache, que producen un concentrador de esfuerzo y la grieta se comporta como un multiplicador de este concentrador.

Para el análisis de la viga se determinó que la grieta de centro es poco probable debido a las cargas que soporta el ala y las características geométricas de las piezas.

Las ecuaciones (10) a la (12) descritas a continuación, fueron usadas en el cálculo teórico de propagación de grieta, siguiendo el modelo de Mecánica de fractura lineal-elásti-ca (Albañil H. Héctor, 2001), (FAATechnical Center, 1993).

Cálculo del factor concentrador β

En la Figura 10 se puede visualizar los 4 tipos de grieta que se presentan en la mecánica de fractura lineal elástica, se tuvieron en cuenta para este análisis solo las últimas tres mostradas en la figura 10, para cada uno de los tipos de grieta el factor concentrador de esfuerzo (3 varía debido a la naturaleza de la grieta y geometría del componente.