Un problema de altura en las operaciones aéreas

rev.ciencia.poder.aéreo.6: 36 - 41, 2011.

Fecha recepción: 29 de marzo de 2011.
Fecha aceptación: 12 de Julio de 2011.

Diego Gerardo Roldán Jiménez¹

Resumen

Mostraremos cómo la probabilidad elemental se puede aplicar a un problema de ataque aéreo a objetivos en tierra. Discutiremos algunos elementos de probabilidad discreta, y plantearemos una situación donde hay un objetivo enemigo en tierra, y necesitamos destruirlo de manera óptima, es decir, con el menor número de bajas aliadas.

Palabras Clave: Bombardeos a objetivos estáticos, modelación matemática, probabilidad.

Abstract

We will discuss how the elementary probability can be applied to a problem of air attack on ground targets. We will argue about some elements of discrete probability, and stand a situation in which there is an enemy target on ground needed to be destroyed optimally with the least amount of allied casualties.

Key Words: Bombing problem, mathematical modeling, probability.

_______________________________________

¹Matemático de la Universidad Nacional de Colombia. Ingeniero Aeronáutico de la Fundación Universitaria Los Libertadores. Estudiante Maestría en Ciencias-Matemática Aplicada - Universidad Nacional de Colombia.

___________________________________________________________________________________________________

Introducción

En los conflictos donde es importante destruir posiciones estratégicas enemigas, es de gran importancia contar con un elemento aéreo aliado que las destruya y así debilitar al enemigo. Principalmente hay dos maneras de atacar un blanco en tierra desde el aire: La primera consiste en realizar una operación aérea donde se envíen aeronaves cuyo armamento principalmente son bombas que son lanzadas a cierta altura sobre el objetivo; este es el caso de operaciones realizadas por los aliados durante la segunda guerra mundial (Barnier, W). La segunda forma consiste en el lanzamiento de misiles a gran distancia (misiles intercontinentales), que con la ayuda de satélites identifica al objetivo y guían al misil hasta él. Naturalmente cada una de estas dos opciones tienen sus ventajas y desventajas, por mencionar algunas: consideremos que para la primera opción existe el riesgo de pérdidas de la tripulación de los bombarderos, mientras que en la segunda no. Por otra parte, si el enemigo cuenta con un arma de detección oportuna de misiles, dependiendo de su efectividad, podrá destruir el misil intercontinental lanzado, mientras que para un ataque masivo de aeronaves sta arma será obsoleta. Vamos a presentar un caso específico de la primera opción, donde lanzamos una ofensiva aérea de bombarderos, y determinamos el menor número de bajas posible.

1. Elementos de Probabilidad

Las probabilidades son los valores de una función de conjunto, también conocida como medida de probabilidad (Billingsley, P.) ya que esta función asigna números reales a los diversos subconjuntos de un espacio muestral S. Mostraremos los postulados de probabilidad donde el espacio muestral S es discreto.

Postulado 1. La probabilidad de un evento es un número real no negativo; esto es, P(A) 0 para cualquier subconjunto A de S.

Postulado 2. P(S) = 1

Postulado 3. Si es una secuencia finita o infinita de eventos mutuamente excluyentes de S, entonces:

Los postulados no requieren demostración, pero si se va a aplicar la teoría resultante debemos demostrar que se satisfacen los postulados cuando damos a las probabilidades un significado real (Carlson, s.f.).

Un ejemplo clásico de probabilidad es cuando queremos determinar el resultado en el lanzamiento de una moneda, para ilustrar este hecho consideremos el siguiente ejemplo:

Ejemplo 1. Si lanzamos dos veces una moneda legal; ¿Cuál es la probabilidad de sacar al menos una cara?

Solución.

El espacio muestral es S_M={S5, 5C,C5,CC} donde C denota cara y S denota sello. Puesto que suponemos que la moneda está balanceada, estos resultados son igualmente posibles y asignamos a cada elemento de la muestra una probabilidad de Sea A el evento que sacamos al menos una cara, obtenemos que a es así:

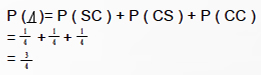
Si en un experimento en el que podemos suponer probabilidades iguales para todos los puntos de muestra, como el caso del ejemplo anterior, podemos hacer uso del siguiente teorema:

Teorema 1.

Si un experimento puede resultar en cualquiera de N resultados diferentes igualmente probables, y si n de estos resultados juntos constituyen el evento A, entonces la probabilidad del evento A es:

La demostración del teorema se puede consultar en Billingsley.

El anterior teorema es congruente con los postulados de probabilidad, resulta de los postulados en el caso especial donde los resultados individuales son todos equiprobables.

1.1 Eventos independientes

Definición 1. Si A y B son dos eventos cualquiera en un espacio muestral la probabilidad condicional de B dado A es

Si consideramos la definición anterior y multiplicamos a ambos lados de la ecuación dada, obtenemos la siguiente Regla de multiplicación:

Teorema 2. Si A y B son dos eventos cualquiera en un espacio muestral , entonces

En palabras, la probabilidad de que A y B ocurran ambos es el producto de la probabilidad de A y la probabilidad condicional de B dado A.

Para considerar dos eventos A y B, de manera informal diremos que son independientes. Si la ocurrencia o no ocurrencia de cualquiera de los dos no afecta la probabilidad de la ocurrencia del otro. Con símbolos, dos eventos A y B son independientes si y se puede demostrar que cada una de estas igualdades implica la otra cuando ambas probabilidades condicionales existen, esto es cuando ni P(A) ni P(B) es igual a 0. Ahora si sustituimos P(B) por en la ecuación del teorema 2, obtenemos

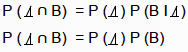
y usaremos esto para mostrar la definición formal de independencia.

Definición 2. Dos eventos A y B son independientes si y solo si

Siguiendo los pasos en sentido inverso, podemos mostrar que la definición 2 implica la definición de independencia que dimos anteriormente.

2. En busca del objetivo

El problema que vamos a considerar es el siguiente: tenemos un número disponible de bombarderos, enviamos todos los bombarderos a destruir el objetivo, el cual está defendido con diferentes armas, por ejemplo lanza-cohetes (de alcance medio) y misiles. Necesitamos garantizar el éxito de la operación, con el menor número de bajas. ¿Cómo modelamos este problema? Fijemos el problema con datos numéricos: supongamos un total de 16 bombarderos enviados a la misión. Ellos necesitan penetrar las defensas aéreas para llegar a su objetivo en tierra. Cada uno de ellos puede volar bajo (máxima altura sobre el terreno 400 ft) y exponerse cada uno a defensas anti-aéreas de corto alcance, volar a una altura media y exponerse a armas de corto alcance y misiles tierra-aire o volar en grandes altitudes (alturas sobre el terreno desde 30.000 ft) y exponerse solamente a los misiles tierra-aire. Es obvio que no queremos enviar aeronaves a volar a una altura media, por que se estaría exponiendo de manera absurda a las aeronaves. Es mejor enfrentar una defensa anti-aérea a dos. Por otra parte, podemos observar que si las aeronaves vuelan a baja altura estarán menor tiempo expuestas a fuego enemigo, caso opuesto con lo que sucede con vuelo a gran altura donde estarán expuestas mayor tiempo a fuego enemigo (ver figura 1).

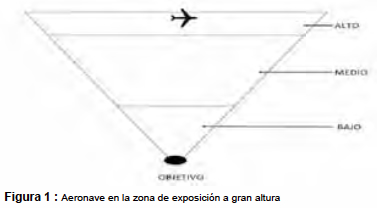
En cada caso la defensa anti-aérea procede en tres etapas:

i) Primero deben detectar la aeronave, después
ii) ubicarla en la mira, y finalmente
iii) dispararle.

Cada una de las etapas puede suceder o no, dependiendo de diversos factores como si la aeronave siguió una ruta constante ó si maniobro y salió del radar, etc. De acuerdo con inteligencia las probabilidades de que un sistema anti-aéreo localice, rastree e impacte una aeronave están dadas por los valores de la tabla 1:

Tabla 1. Probabilidad de las etapas de las defensas anti-aéreas.

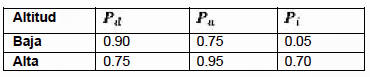
donde P_dl es la probabilidad de localización, P_dr probabilidad de rastreo, y P_i probabilidad de impacto. En una misión previa de inteligencia se determinan las capacidades del enemigo en tierra. Se sabe que dispone de armas de corto alcance (lanza-cohetes) que pueden disparar una ronda de 20 cohetes por minuto, y que dispone de una instalación de misiles de largo alcance que puede disparar 3 misiles por minuto. En el plan de vuelo se sugiere que las aeronaves se expongan por 1 minuto si ellos vuelan en formación de baja altitud y 5 minutos si ellos vuelan a gran altura. Estos valores se mantienen sin importar si el ataque aéreo es diurno o nocturno. Necesitamos determinar la trayectoria de vuelo óptima (baja o alta altitud). El objetivo es maximizar el número de bombarderos que sobrevivan al ataque.

3. Trayectoria Óptima

Determinamos la probabilidad de que un proyectil impacte una aeronave, para ello observamos que,P_dl , P_dr y P_i son independientes, así: P_impac to = P_dl P_dr P₁

Y fijamos el número de aeronaves que serían destruidas como N_D que depende del tiempo de exposición R , y la cantidad de munición lanzada por minuto:

C:
N_D = RCP _impacto

Esto determina que para el vuelo a alta altitud serian destruidas siete aeronaves y a baja altitud solo una, por eso es más factible viajar a baja altitud.

Cada bombardero utilizado en la operación tiene una P =70% de probabilidad de destruir el objetivo.

Determinemos la probabilidad de que todos los bombarderos destruyan el objetivo de manera conjunta: la probabilidad de que el objetivo sobreviva a un ataque individual está dado por q = 1 - p

Como en total sobreviven N = 15 aeronaves, entonces la probabilidad de que el objetivo en tierra sobreviva será:

P_sobrevivir = qⁿ

Tenemos que P_sobrevivir es casi cero. Luego en este caso la operación es un éxito.

Entre las ideas de una planificación aérea exitosa, está la utilización de la menor cantidad de recursos. Miremos cómo determinamos la cantidad mínima de bombarderos para garantizar un éxito del 95 %.

Suponemos que sobreviven un total de bombarderos a las defensas anti-aéreas, entonces la probabilidad del éxito de la operación está dada por P_dr = 1 - 0 . 3^m y tenemos que P_dr 0 . 9 5 siempre que m 3 .

Entonces suponiendo un vuelo a baja altitud donde derriban una aeronave, tenemos que el número mínimo de aeronaves enviadas a la misión será N = 4.

Diseñemos un análisis de sensibilidad con respecto a la probabilidad p = 0 . 7 de que una aeronave destruya un objetivo.

Esto se hace para determinar la cantidad de aeronaves que deben usarse cuando P cambia. Este valor cambia de acuerdo con varios factores, como la precisión de los dispositivos utilizados en las aeronaves, la dificultad de acceso al terreno entre otros. Consideramos el número de bombarderos que deben ser enviados para destruir el objetivo con una efectividad de P = 0 , 9 5 . Procedamos de la siguiente forma: Consideremos la fórmula general de destruir el objetivo con una probabilidad del 95%

Como se espera perder una aeronave en la misión, pensamos enviar N = m + 1 aeronaves a la misión, así el número de aeronaves varía con la probabilidad de éxito de acuerdo con los resultados mostrados en la tabla 2.

Tabla 2. Número de aeronaves y probabilidad de éxito.

Diversos factores como el polvo en el aire, y el mal tiempo reduce la probabilidad de que el bombardero sea detectado P_dL y la probabilidad p de éxito de cada aeronave.

Si ambas probabilidades se reducen a la misma proporción ¿Cuál bando tendrá la ventaja del mal tiempo?

Cuando existe un sistema de baja presión es muy probable que no se realice la operación porque eso atenta la seguridad aérea, entonces en esta situación para lograr un éxito del 95% se necesitarán 7 aeronaves; es decir 3 aeronaves más involucrando un gasto mayor de recursos. Luego la situación del mal tiempo, favorecerá al enemigo y por lo tanto, no debe realizarse la operación aérea.

Conclusiones

Muchos problemas de la vida real contienen elementos de incertidumbre, para este caso el ataque a un objetivo observamos que hay varios elementos sobre los cuales no podemos tener control.

Observamos que de manera conveniente establecimos una distribución de probabilidad para establecer un modelo matemático que nos ayude a tener cierto dominio sobre la situación planteada.

Concluimos que además de conocer el número de aeronaves que sobreviven al ataque, podíamos determinar el número enviado a la misión con el fin de optimizar recursos, los cuales son muy importantes en una situación crítica como lo es una guerra.

La situación planteada puede ser modificada, para asemejarse a una situación real, incluyendo varias variables como la velocidad de las aeronaves y misiles, efectividad de las bombas lanzadas, alcance de radar, tipo de terreno, probabilidades de detección e impacto (Roldán) donde los datos se obtienen de fuentes de inteligencia, y así optimizar el ataque aéreo.

Referencias

Barnier, W (s.f). Expected Loss in Keno. Módulo 574.

Billingsley, P. (1979). Probability and measure. Wiley: New York.

Carlson. Conditional Probability and Ambiguous information. Módulo UMAP. 391.

Bender, E. A. An introduction to Mathematical Modeling. New York: Wiley & Sons.

Ross, S. (s.f.). Introduction to probability models. 3rd ed. New York: Academic Press.

Feller, W. (1971). An introduction to probability theory and its applications. Vol. 2 2nd ed. New York: Wiley.

Roldán, D. G. (2011). Modelación de una Operación Aérea.Working Paper.

Meerschaert, M. (1993). Mathematical Modeling, Academic. New York: Press Inc.

Dym, C. L. Principles of Mathematical Modeling. California: Claremont.