Modelación matemática de una operación aérea de búsqueda

Mathematical modeling of an aerial search operation

rev.ciencias.poder.aereo.8:21-25, 2013

Recibido: 25/04/2012
Aprobado evaluador interno: 01/09/2012
Aprobado evaluador externo: 02/08/2013

Diego Gerardo Roldán Jiménez³
Jorge Mauricio Ruíz⁴

Resumen

En este artículo se planteará un modelo de distribución de aeronaves de rescate, en una zona geográfica determinada, donde se cree desaparecida una aeronave. En la operación descrita se determinará la cantidad necesaria de aeronaves de búsqueda que deben utilizarse en la operación y la forma cómo deben distribuirse sobre la zona geográfica para maximizar la probabilidad de encontrar la aeronave desaparecida utilizando elementos de la probabilidad clásica.

Palabras clave: Modelación matemática, operaciones aéreas de búsqueda, probabilidad.

Abstract

This article considers a distribution model for rescue aircraft in a search operation for missing aircraft in a given geographical area. The article determines how many search aircrafts should be deployed for the operation described and how they should be geographically distributed in order to maximize the probability of finding the missing aircraft using elements of classical probability

Key Words: Aerial Search Operations, Mathematical Modeling, Probability.

_______________________________________

¹Artículo corto producto de un trabajo de investigación en Matemáticas Aplicada en la Universidad Nacional de Colombia.
²Short article, product of an investigative project in Applied Mathematics in the National University of Colombia.
³Msc. en Matemática Aplicada. Facultad de Ciencia y Tecnología, Universidad de Ciencias Aplicadas y Ambientales.
⁴Ph.D. en Matemáticas. Departamento de Matemáticas, Universidad Nacional de Colombia.

___________________________________________________________________________________________________

1. Introducción

Las operaciones de búsqueda y rescate son muy importantes durante sucesos donde se reportan personas ó aeronaves extraviádas. En un infortunio como estos, se debe primero analizar la posible región donde se cree hay personas ó aeronaves desaparecidas.

Este estudio de la región contempla diferentes factores como por ejemplo: las coordenadas, el clima, el terreno, la altitud, la vegetación entre otras. A pesar de que una operación de búsqueda y rescate está planificada de manera casi inmediata, en ocasiones no es posible realizar estas misiones por factores como disponibilidad de aeronaves ó en el caso más típico por las condiciones climáticas.

Por ejemplo, en una operación de búsqueda y rescate en una cordillera existe la posibilidad de nubosidad, lluvias, y vientos cruzados. Así estas operaciones dependen principalmente del clima que predomina sobre la región de la búsqueda.

En un sector de búsqueda, en la mayoría de los casos se realizan sobrevuelos con el fin de determinar el punto exacto donde sucedió la tragedia en el caso de una aeronave estrellada (ó la localización exacta de personas desaparecidas). Después se procede a enviar grupos de rescatistas que dependiendo del acceso a la zona se dirigen caminando ó descendiendo de helicópteros.
También, existe la posibilidad de que el tamaño de los helicópteros no permita su uso en la zona de búsqueda. Para ello, se simplifica el modelo considerando aeronaves de características similares.

Para plantear el modelo de distribución de aeronaves de rescate, en una región donde se cree desaparecida una aeronave, se deben considerar algunos supuestos, tales como:

• Helicópteros de búsqueda de las mismas características.
• Características del terreno donde se cree está la aeronave desaparecida. Esto es se conocen la vegetación y el clima de la zona ya que con estos datos es posible fijar porcentajes de éxito de encontrar la aeronave en regiones determinadas del terreno.
• Cada helicóptero encuentra a la aeronave de forma independiente

Con estas suposiciones iniciales, se plantea un modelo probabilístico que describa la manera óptima de distribuir los helicópteros de tal forma que esta distribución permita hallar la aeronave desaparecida con alta probabilidad de éxito.

2. Modelo

Cuando las probabilidades se citan sin especificar el espacio muestral S pueden aparecer fácilmente dificultades. En muchas situaciones el resultado de un experimento depende de lo que sucede en varias etapas intermedias. Para este artículo el interés está en considerar la situación donde las etapas intermedias permiten n diferentes (cuya ocurrencia se nota por B₁, B₂, ..., B_n. Se requiere del siguiente teorema conocido como el teorema de probabilidad total.

Teorema 1 (Ross, 2009)

Sea B₁, B₂, ..., B_n. una partición sobre el espacio muestral S y sea A un evento cualquiera del que se conocen las probabilidades condicionales P(AIB_i) entonces la probabilidad del evento del evento A viene dada por la expresión:

2.1. Situación

Sin perdida de generalidad, se puede suponer una región de búsqueda cuadrada tal como se ilustra en la Figura 2. En principio se puede considerar una región de este tipo, donde cada cuadrícula consiste en un sector específico, al cual se deben enviar una cantidad de helicópteros determinados. Esta ilustración es bastante útil ya que a cada sector de la región dada, se le puede asignar una determinada probabilidad de que la aeronave desaparecida esté en este sector. De esta forma si se toma una región S de n fila y n columnas, tal que se pueda asignar una probabilidad p_ij con i,j I = {1,2...,n} de que la aeronave se encuentre en el sector de la fila i- ésima y la columna j- ésima, podemos construir una matriz de probabilidades C:

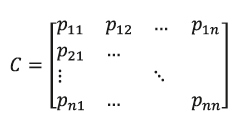
Escrito de una manera mas formal, si B_ij representa el evento: B_ij = la aeronave extraviada está en el sector ij

Se tiene que P(B_ij) _pi con i,j I. Si N = n x n es decir N es la totalidad de sectores de búsqueda en la región S, se puede concluir.

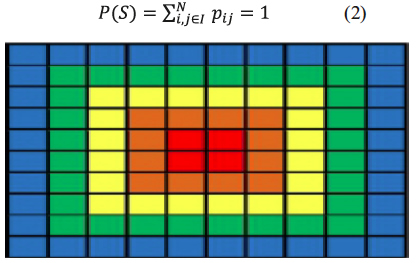
Figura 1.División de una zona de S búsqueda de 10 filas y 10 columnas

Una vez descrita la región de búsqueda, la pregunta que se plantea es:

¿Cómo distribuir los helicópteros para que la probabilidad de encontrar la aeronave extraviada sea máxima ?

Se nota a x_ij la cantidad de helicópteros que se envían al sector B_ij . Si definimos a A como el evento:

A:= Encontrar la aeronave pérdida

Se debe encontrar una expresión que permita determinar los valores de x_ij con i, j I tal que P(A) sea máxima. En este caso se utiliza el teorema de probabilidad total para obtener la siguiente expresión:

donde P(B_ij ) = _pij y por el teorema del complemento de probabilidades:

para i, j I. Además si un helicóptero tiene una probabilidad p de encontrar una aeronave, entonces

representa la probabilidad de que el helicóptero no encuentre la aeronave, así suponiendo independencia de eventos, la probabilidad de que en un sector B_ij un total de x_ij helicópteros no encuentren la aeronave pérdida está dada por:

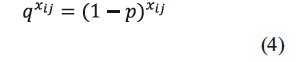
luego:

entonces la expresión para determinar la probabilidad de encontrar la aeronave está dada por:

En la anterior ecuación se deben encontrar los valores de x_ij tal que P(A) tome su valor máximo. En el siguiente ejemplo se mostrará más detalladamente de qué manera la ecuación (5) permite determinar cómo distribuir helicópteros sobre una región donde se cree desaparecida una aeronave.

Ejemplo 1. En el centro de operaciones aeronáuticas se determinó que en una región S se ha extraviado una avioneta. De acuerdo a las condiciones del terreno y a las condiciones climáticas se determinó que era suficiente considerar una división del terreno S entre sectores: B₁, B₂ y B₃, con la probabilidad de encontrar la avioneta en cada sector con éxito del 30%, 20% y 50% respectivamente. En la base aérea se dispone de 7 helicópteros con las mismas características que son dispuestos para realizar la búsqueda. Por experiencia de las tripulaciones y de acuerdo a las condiciones climáticas cada helicóptero se fija con un 15% de probabilidad de encontrar la avioneta pérdida. ¿Cómo se deben distribuir los helicópteros en la región de tal forma que la probabilidad de encontrar la avioneta sea máxima?

Para encontrar la forma de como distribuir los helicópteros, primero se deben considerar los siguientes eventos:

La región de búsqueda se puede describir utilizando la siguiente matriz de probabilidades:

además N = 3 por que sólo se consideran 3 sectores en la región S; así:

También se sabe que:

entonces se puede simplificar (6) tal que:

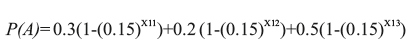
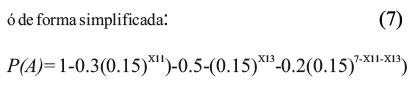
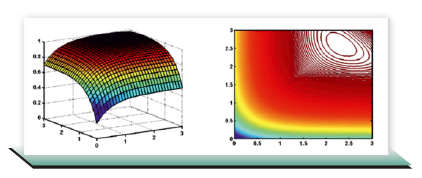
Figura 2. Gráfica de P(A) y curvas de nivel. Este ejemplo se solucionó con MATLAB, aunque en el mercado existen diferentes paquetes con múltiples opciones para solucionarlo.

Para la ecuación (7) se encuentran los puntos críticos y dos máximos en:

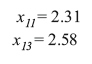
Por lo tanto x₁₂ = 2.11. Y como se consideran = x₁₁ , x₁₂ y x₁₃ números naturales, se tiene que:

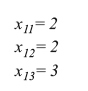
Así, se concluye que deben enviar dos helicópteros al sector 1 y al sector 2, y tres helicópteros al sector 3. Y con esta distribución se tendrá una probabilidad de encontrar la avioneta del 98%.

Ejemplo 2. La óptimización de recursos es muy importante en las operaciones aéreas. Si para el ejemplo anterior se quiere una probabilidad de encontrar la aeronave con un 98% y suponiendo que la cantidad de helicópteros enviados a B₁ y B₂ son los mismos. ¿Cuál es la cantidad mínima de helicópteros requeridos en la misión ?

Se modifica la ecuación (7) tal que P(A) = P₀ = 95% Nótese como N₀ la cantidad de helicópteros necesarios para la misión, así que con las simplificaciones asumidas se obtiene la siguiente expresión:

Esta es una importante restricción a utilizar en el ejemplo, ya que para garantizar la misión con probabilidad P₀ el número de aeronaves x₁₁ debe satisfacer tal desigualdad.

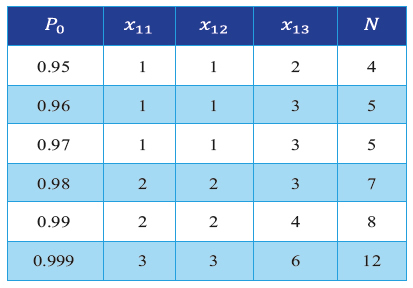
En la siguiente tabla se ilustra la cantidad de aeronaves necesarias para la operación y diferentes valores de P₀ . Tal como es de esperarse, si se envían más helicópteros a la misión las probabilidades de encontrar la avioneta desaparecida aumentan.

Tabla 1.Helicópteros requeridos para diferentes probabilidades P₀

3. Conclusiones

En las operaciones de búsqueda y rescate, la asistencia, traslado de equipos y personal a la zona de operaciones, debe realizarse de manera casi inmediata al reporte de la emergencia, este es el tiempo de reacción de las tripulaciones, muy importante para estas misiones. Además, dependiendo de las características de la tripulación y de las aeronaves es posible fijar probabilidades que permitan determinar éxito en la búsqueda.

Cuando se fijan estas probabilidades se deben considerar múltiples factores asociados a la naturaleza, a destacar las condiciones meteorológicas (que influyen de manera directa, ya que si las condiciones climáticas no son las apropiadas es muy difícil que una tripulación entrenada tenga altas probabilidades de tener éxito en la misión); también se tienen en cuenta las condiciones del terreno: no es lo mismo hacer una búsqueda en una zona selvática a una zona desértica.

El modelo indica que las probabilidades de encontrar una aeronave, aumentan si se dispone de mayores recursos, es decir más aeronaves. También, este modelo permite considerar regiones irregulares en geometría superficial. Esta situación se presenta cuando se consideran regiones de búsqueda mayores debido a la falta de información en la operación.

Referencias

Barnier W. (1986).Expected Loss in Keno, modulo 5 7 4 : UMAP.

Bender E.A. (2000). An introduction to Mathematical Modeling.New York:Wiley & Sons.

Billingsley P.(1979). Probability and measure, Wiley, New York.

Carlson.(1971).Conditional Probability and Ambiguous information.UMAP modulo 391.

Clive L. Dym. (2004).Principles of Mathematical Modeling. Claremont, California.

Feller W. (1971). An introduction to probability theory and its applications, Vol. 2.

Meerschaert M. (1993) Mathematical Modeling, Academic.New York: Press Inc.

Ross S. (2009). Introduction to probability models, 3rd ed. New York: Academic Press.