Simulación de la trayectoria de un cohete de dos etapas para posicionamiento de un nanosatélite en órbita
Simulation of a Two Stage Rocket Trajectory to Place a Nanosatellite into Orbit
3Jhonathan Orlando Murcia Piñeros
4José Gregorio Portilla Barbosa
Recibido: 29/09/2013
Aprobado evaluador interno: 09/10/2014
Aprobado evaluador externo: 12/11/2014
Resumen: En el presente artículo se estudia el posible lanzamiento de un cohete de dos etapas impulsado por propelentes líquidos tipo RP-1 para transportar una carga útil de 4 kg equivalente a la masa de un nano-satélite de tres unidades de Cubesat. Se plantea el estudio con el diseño conceptual del cohete portador implementando un código computacional de optimización con la finalidad de reducir la masa al despegue y aumentar la velocidad. Se eligió como sitio de lanzamiento desde Colombia a la base del Grupo Aéreo del Oriente (GAORI) en Marandúa, Vichada, dado que en la actualidad se realizan investigaciones en lanzamiento de cohetes y ha sido utilizado por universidades para el desarrollo de tales investigaciones. Los valores obtenidos anteriormente son introducidos en un código computacional en FORTRAN desarrollado en el Observatorio Astronómico de la Universidad Nacional de Colombia para obtener el comportamiento de la trayectoria de vuelo del cohete durante su fase de ascenso e inyección orbital.
Palabras clave: Cohete líquido, nanosatélite, órbita baja, trayectoria de vuelo.
Abstract: This article aims to study the possibility of launching a two-stage liquid propellant rocket in order to put into orbit a 4 Kg payload, equivalent to the mass of a 3U CubeSat. It presents a study with a conceptual design of the carrier rocket implementing a computer optimization code in order to reduce mass and increase takeoff speed. As a launch site the Air Force Base named Grupo Aéreo del Oriente (GAORI) in Marandua, State of Vichada, Colombia, was chosen, due to the fact that there is research in rocketry currently carried out there, and that the place has been used by universities for development of such investigations. Results were input into a computer code in FORTRAN developed at the National Astronomical Observatory of the National University of Colombia in order to study the flight path of the rocket during its ascent phase and entrance into orbit.
Key Words: Flight Path, Liquid Rocket, Low Earth Orbit (LEO), Nano - Satellite.
____________________________________________________
3 Ingeniero Aeronáutico con Maestría en Ciencias Astronomía, Observatorio Astronómico Nacional, Universidad Nacional de Colombia. Estudiante de Doctorado en Ingeniería y Tecnologías Espaciales – Mecánica Espacial y Control.
4 PhD. Director del Observatorio Astronómico Nacional. Universidad Nacional de Colombia.
Introducción
Los nanosatélites (entre los que se encuentran los Cubesats) han sido utilizados a nivel mundial para la realización de experimentos asequibles económicamente y por su relativa facilidad en su montaje y colocación en órbita. Colombia ha incursionado en esta área con el desarrollo y colocación en órbita del Libertad 1 (realizada en el año 2007) por parte de la Universidad Sergio Arboleda (Joya, 2007). En la actualidad se adelantan proyectos en el desarrollo de nuevos picosatélites con aplicaciones en medicina como es el caso de la Universidad Distrital Francisco José de Caldas. También está en fase de desarrollo el picosatélite Libertad 2 de la Universidad Sergio Arboleda.
La Fuerza Aérea Colombiana (FAC) ha propuesto también el desarrollo de un nanosatélite (FACSAT 1) conformado por tres unidades de picosatélites con una masa cercana a los 4 kg. Igualmente, planea la construcción de un cohete portador para el posicionamiento futuro de esos pequeños satélites (Gutiérrez, 2012). Motivados principalmente por estas últimas iniciativas exponemos en esta comunicación el estudio de la simulación del lanzamiento de un cohete desde territorio colombiano para la colocación de un nanosatélite.
Satélites
Una parte decisiva de la incursión de un país en materia de investigación espacial para efectos de generar y consolidar independencia tecnológica, consiste en su firme propósito de desarrollar y construir cargas útiles a transportar y, más importante aún, colocarlas por sus propios medios en órbita. Como es de esperarse, solo países tecnológicamente avanzados se han dado a esta tarea, aunque, si se tiene en cuenta lo que al respecto han realizado naciones como India y Corea del Norte y, próximamente Brasil y Argentina, indican que lo que se requiere, más que tecnología (que, por supuesto, es importante), es la decisión política de hacerlo. Es evidente que la realización de este tipo de objetivos no sólo genera prestigio, también, bien administrado, generará reditos significativos para el país. A manera de ejemplo: en la actualidad, la industria de construcción de satélites en el mundo desarrollado supera los 160 miles de millones de dólares y solo en los Estados Unidos da empleo a casi 27000 personas5
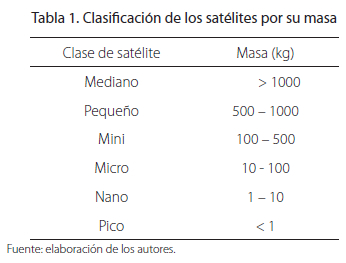
Los satélites se suelen clasificar de acuerdo a su masa, tipo de órbita y misión a desarrollar. En esta última clasificación se pueden dividir en satélites de comunicación (tanto militares como civiles), observación de la Tierra, meteorológicos, vigilancia, navegación, investigación astronómica, entre otros (Fortescue, Stark y Swinerd, 2003). Una clasificación, esta vez por masa, puede observarse en la Tabla 1.
Los denominados nanosatélites son en la actualidad ampliamente utilizados para diversos propósitos y suelen posicionarse en órbitas bajas (LEO, por Low Earth Orbit). El interés en su desarrollo, construcción y uso radica en que representan bajos costos de operación, fabricación y lanzamiento (Fortescue, Stark y Swinerd, 2003).

Cohete portador
El cohete portador o lanzador es un vehículo impulsado por motores cohetes que tiene la capacidad de transportar una carga útil desde la superficie de la Tierra a órbitas alrededor de ésta. Para lograr su objetivo requiere alcanzar velocidades del orden de la decena de kilómetros por segundo y que dicha velocidad sea transmitida a la carga útil para que, de ese modo, quede en órbita elíptica alrededor de la Tierra.
La velocidad del cohete puede calcularse, en un buen grado de aproximación y sin tener en cuenta las pérdidas por gravedad y fuerza de arrastre atmosférico, por medio de la ecuación de Tsiolkovsky (Ecuación 1), la cual depende de la velocidad de salida de los gases en la tobera ![]() y la relación de masas finales
y la relación de masas finales ![]() e iniciales
e iniciales ![]() (Sutton y Biblatz, 2010), así:
(Sutton y Biblatz, 2010), así:
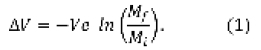
De forma realista, el cohete debe atravesar la atmósfera terrestre donde se generan fuerzas aerodinámicas por el movimiento a través del fluido. Obviamente, está sometido a la atracción gravitacional ejercida por el planeta y, por supuesto, al empuje generado por los motores cohete. El desarrollo de este tipo de vehículos es otro paso fundamental que una nación debe dar para ser independiente en el campo espacial y posicionar los satélites que requiera y construya. De existir un esfuerzo decidido, Colombia podría contar con la capacidad de desarrollar motores cohete de propelentes líquidos consistentes en oxígeno líquido y keroseno los cuales pueden generar un impulso especifico (lsp) cercano a los 320 segundos mediante una relación de oxidante/combustible (LOX/ RP-1) de 2.0 (Humble, Henry y Larson, 1995).
Puesto que el propósito de la nación, a un mediano plazo, es colocar cargas útiles de 4 kg a órbitas bajas, puede determinarse en primera aproximación un cambio de velocidad total para la misión de ![]() = 8.4 km/s, basado en parámetros estadísticos de diversos cohetes portadores a nivel mundial. Este es el cambio de velocidad neta que debe efectuar el propelente de un cohete ideal según la Ecuación (1), teniendo en cuenta un promedio estadístico de las pérdidas por velocidad merced a la influencia del campo gravitacional de la Tierra y el arrastre atmosférico (Humble, Henry y Larson, 1995). Obedeciendo razones de simplificación en desarrollo tecnológico, costos y minimización de probabilidad de fallas, se escogió, para este análisis, un cohete conformado por solo dos etapas.
= 8.4 km/s, basado en parámetros estadísticos de diversos cohetes portadores a nivel mundial. Este es el cambio de velocidad neta que debe efectuar el propelente de un cohete ideal según la Ecuación (1), teniendo en cuenta un promedio estadístico de las pérdidas por velocidad merced a la influencia del campo gravitacional de la Tierra y el arrastre atmosférico (Humble, Henry y Larson, 1995). Obedeciendo razones de simplificación en desarrollo tecnológico, costos y minimización de probabilidad de fallas, se escogió, para este análisis, un cohete conformado por solo dos etapas.
Se procedió entonces a fijar los valores de impulso específico, cambio de velocidad y masa de la carga paga en un código computacional iterativo aplicando el método de Newton-Rhapson, desarrollado por los autores, encargado de optimizar el diseño conceptual del cohete portador. Con ello, se busca minimizar la masa al despegue y aumentar el cambio de velocidad (Tewari, 2006). Puesto que, por definición, la velocidad de los gases de escape es igual al producto del impulso específico (lsp) con la aceleración gravitacional en la superficie terrestre ![]() se puede escribir la Ecuación (1) como:
se puede escribir la Ecuación (1) como:
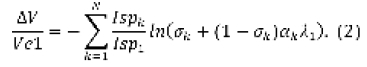
Los subíndices ![]() indican los números de etapas del cohete (en nuestro caso N=2),
indican los números de etapas del cohete (en nuestro caso N=2), ![]() es la relación de masa estructural; para este caso 0.1 indicando que el 10% del peso total de la etapa corresponde a la estructura;
es la relación de masa estructural; para este caso 0.1 indicando que el 10% del peso total de la etapa corresponde a la estructura; ![]() es la relación de factores de carga y
es la relación de factores de carga y ![]() la relación entre la masa inicial y la carga útil.
la relación entre la masa inicial y la carga útil.
Adoptando como lsp= 320 s para ambas etapas, un valor de masa útil de 4 kg y ![]() = 8.4 km/s, se procedió a resolver la Ecuación (2) mediante un proceso de iteración. De ese modo se obtienen las masas correspondientes a cada etapa, sus estructuras y propelente que integran el cohete portador ya optimizado (ver Tabla 2).
= 8.4 km/s, se procedió a resolver la Ecuación (2) mediante un proceso de iteración. De ese modo se obtienen las masas correspondientes a cada etapa, sus estructuras y propelente que integran el cohete portador ya optimizado (ver Tabla 2).
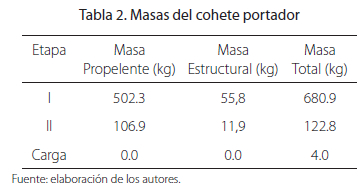
Con las masas iniciales de cada etapa se determinó la fuerza de empuje a partir de la relación adimensional empuje/peso ![]() para los cohetes portadores. Esta relación, para los cohetes existentes, suele oscilar entre un valor de 1.0 a 1.5 para las primeras etapas y de 0.8 a 1.2 para etapas subsecuentes (Humble, Henry y Larson, 1995). Para el caso que nos ocupa, determinamos un valor medio de 1.3 y de 1.0, para la primera y segunda etapa, respectivamente. Aplicando la Ecuación (3) se puede hallar el flujo másico
para los cohetes portadores. Esta relación, para los cohetes existentes, suele oscilar entre un valor de 1.0 a 1.5 para las primeras etapas y de 0.8 a 1.2 para etapas subsecuentes (Humble, Henry y Larson, 1995). Para el caso que nos ocupa, determinamos un valor medio de 1.3 y de 1.0, para la primera y segunda etapa, respectivamente. Aplicando la Ecuación (3) se puede hallar el flujo másico ![]() (donde el punto sobre la letra representa la primera derivada con respecto al tiempo
(donde el punto sobre la letra representa la primera derivada con respecto al tiempo ![]() ) considerando una fuerza de empuje constante a través de la ecuación que define el empuje en el vacío:
) considerando una fuerza de empuje constante a través de la ecuación que define el empuje en el vacío:
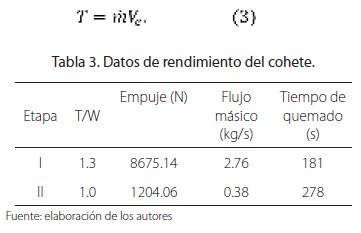
Con la anterior ecuación se determinaron los valores de tiempo de quemado de los motores, asumiendo ![]() constante (con un valor distinto para cada una de las dos etapas), los cuales están consignados en la Tabla 3.
constante (con un valor distinto para cada una de las dos etapas), los cuales están consignados en la Tabla 3.
Teniendo en cuenta, las masas de propelente, densidad de los mismos y parámetros históricos de los cohetes, se pueden determinar las dimensiones generales para el cohete. En el presente caso se obtuvo un cohete con un diámetro de 0.5 m y longitud de 6.0 m. Conceptualmente se puede elegir una ojiva de tipo cónico y cuatro aletas trapezoidales. Para hacer más refinadas y realistas las simulaciones esta información geométrica fue introducida en un código computacional para determinar los coeficientes aerodinámicos de arrastre en función del número Mach de acuerdo a parámetros estadísticos de los misiles (Fleeman, 2006).
Ecuaciones de movimiento
El movimiento del cohete está determinado principalmente por la fuerza de empuje en la atmósfera ![]() , ecuación (4), donde
, ecuación (4), donde ![]() es la presión de los gases a la salida de la tobera,
es la presión de los gases a la salida de la tobera, ![]() el área total de ésta y
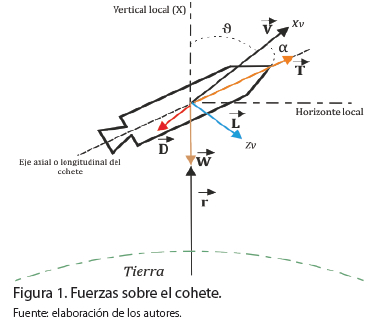
el área total de ésta y ![]() la presión del aire circundante. Esta fuerza actúa sobre el eje axial del vehículo (ver Figura 1). Por otra parte, durante el ascenso, el cohete se desplaza a través de la atmósfera. Esto hace que, sobre el vehículo, actúen dos componentes de fuerza aerodinámica: el arrastre
la presión del aire circundante. Esta fuerza actúa sobre el eje axial del vehículo (ver Figura 1). Por otra parte, durante el ascenso, el cohete se desplaza a través de la atmósfera. Esto hace que, sobre el vehículo, actúen dos componentes de fuerza aerodinámica: el arrastre ![]() , Ecuación (5) y la sustentación
, Ecuación (5) y la sustentación ![]() Ecuación (6). Ambas fuerzas dependen de la densidad del aire,
Ecuación (6). Ambas fuerzas dependen de la densidad del aire, ![]() , la cual cambia con respecto a la altitud, la temperatura y la presión. Para modelar estas fuerzas es necesaria la aplicación de un modelo de atmósfera estándar hasta los 1000 km de altitud (Minzner, Champion y Pond, 1959) dentro del código computacional (Zipler, 2007).
, la cual cambia con respecto a la altitud, la temperatura y la presión. Para modelar estas fuerzas es necesaria la aplicación de un modelo de atmósfera estándar hasta los 1000 km de altitud (Minzner, Champion y Pond, 1959) dentro del código computacional (Zipler, 2007).
Durante todo el vuelo de la misión el cuerpo del cohete se somete a la fuerza de atracción gravitacional ![]() existente entre la masa del vehículo
existente entre la masa del vehículo ![]() la masa del planeta Tierra
la masa del planeta Tierra ![]() (5.97 X 1024 kg), Ecuación (7). Una vez que el cohete abandona la atmósfera terrestre y apaga los motores, la gravedad es la única fuerza que influye en su movimiento.
(5.97 X 1024 kg), Ecuación (7). Una vez que el cohete abandona la atmósfera terrestre y apaga los motores, la gravedad es la única fuerza que influye en su movimiento.
Las ecuaciones de fuerzas sobre el cohete se pueden escribir como:
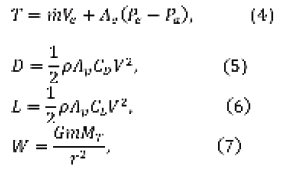
donde ![]() es la masa del cohete r es la distancia entre el centro de la Tierra y el vehículo G la constante de Gravitación (6.67 X 10-11 m3 s-2 kg-1)
es la masa del cohete r es la distancia entre el centro de la Tierra y el vehículo G la constante de Gravitación (6.67 X 10-11 m3 s-2 kg-1) ![]() el área proyectada del vehículo,
el área proyectada del vehículo, ![]() sus coeficientes de resistencia y sustentación, respectivamente (ambos funciones de la forma geométrica del vehículo, de la velocidad
sus coeficientes de resistencia y sustentación, respectivamente (ambos funciones de la forma geométrica del vehículo, de la velocidad ![]() el denominado ángulo de ataque).
el denominado ángulo de ataque).
Teniendo en cuenta las fuerzas que actúan sobre el cohete se puede encontrar la relación entre ellas en la ecuación general del movimiento, Ecuación (8), sin tener en cuenta los términos de aceleraciones generados por la rotación terrestre:
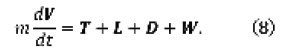
donde V es la velocidad del cohete.
Incluyendo el efecto de la rotación de la Tierra, las seis ecuaciones diferenciales de movimiento adoptan la forma (Tewari, 2006; Weiland, 2010):
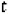
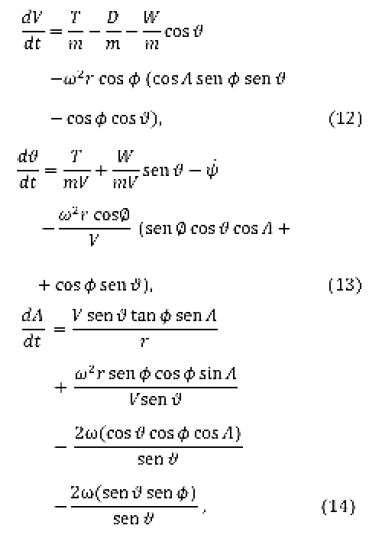
donde ![]() son la latitud y la longitud geográfica, respectivamente,
son la latitud y la longitud geográfica, respectivamente, ![]() es el rumbo o azimut (ángulo medido desde el norte en dirección hacia el este),
es el rumbo o azimut (ángulo medido desde el norte en dirección hacia el este), ![]() es el ángulo de vuelo (ángulo entre el radio vector y el vector velocidad) y
es el ángulo de vuelo (ángulo entre el radio vector y el vector velocidad) y ![]() es la velocidad angular de la Tierra.
es la velocidad angular de la Tierra.
Si bien, en la actualidad existen lenguajes de programación más flexibles y poderosos, tales como C++ y Python, se decidió desarrollar un código en FORTRAN77 para la integración numérica de las ecuaciones diferenciales. La razón fundamental radica en que el integrador base, llamado RADAU, está escrito en tal lenguaje. Aunque desarrollado a finales de los años setenta del siglo pasado, el hecho es que la NASA y otras instituciones en Estados Unidos, siguen utilizando y desarrollando códigos en temáticas aeroespaciales con base en FORTRAN77.
Resultados
Se procedió a simular el lanzamiento de dicho cohete desde la base del Grupo Aéreo del Oriente (GAORI) ubicada en Marandúa. Esta base se seleccionó por la importancia histórica en el campo de la cohetería ya que allí se han realizado (y continúan realizándose) pruebas de funcionamiento de los misiles, cohetes y explosivos de la Industria Militar Colombiana (INDUMIL). También allí se han realizado pruebas de cohetes por parte del Grupo PUA de la Universidad de los Andes y el Centro de Investigaciones Aeroespaciales (CITAE) de la Fuerza Aérea. La base se encuentra localizada a 5°31´35.3” de latitud norte y 68°40´48.7” de longitud oeste, en medio de la selva del Vichada (Urrego, 2009). Adicionalmente, se tiene en cuenta que para el satélite se le ha fijado un área de sección transversal proyectada de 0.01 m2 (área lateral del Nano satélite) y un coeficiente de resistencia de 2.2 (Galli y Rochus, 2008).
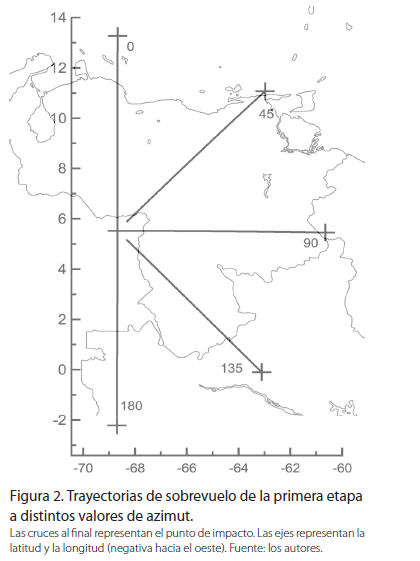
El primer paso en las simulaciones fue la determinación de la caída y zonas de impacto de la primera etapa del cohete lanzado desde GAORI. Para ello se cambió el azimut cada 45° desde los 0° hasta 180°. En la Figura 2 se observa el sobrevuelo de la trayectoria donde las cruces representan las zonas de impacto. Cabe aclarar que, para este caso, se simuló una caída libre de la primera etapa que no tuvo en cuenta la implementación de un dispositivo de frenado aerodinámico (paracaídas) para su recuperación.
Como se observa en la Figura 2, con un azimut de 0° el cohete sobrevuela gran parte del territorio del vecino país de Venezuela, impactando cerca de la isla de Aruba. Para un azimut de 45°, sobrevuela Venezuela e impacta cerca a la isla de Margarita. Con 90° el impacto ocurre cerca de la frontera de Venezuela con Guyana.
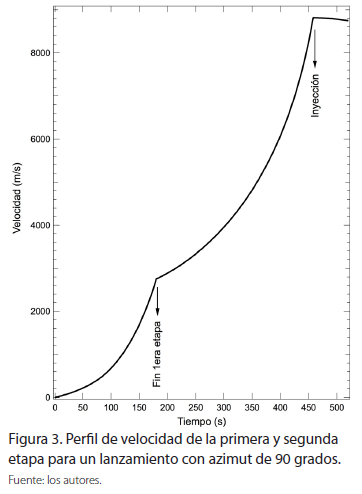
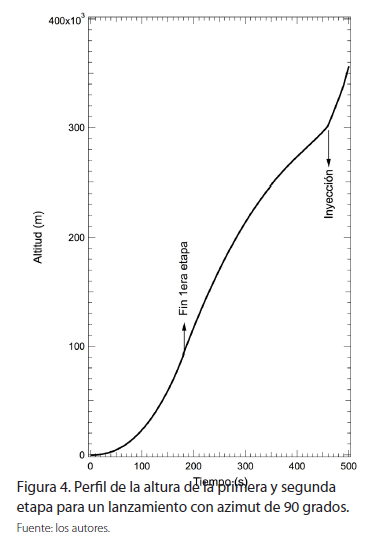
Para las trayectorias comprendidas entre 100° y 160° el cohete sobrevuela territorio venezolano para luego continuar sobrevolando e impactar en la región amazónica de Brasil. Por encima de 160° el sobrevuelo e impacto es solo sobre el Brasil. Basados en estos resultados, se seleccionó primeramente un rumbo medio de 90° para simular una trayectoria de vuelo con inclinación cercana a 0°, es decir, una órbita casi ecuatorial. Para este valor, se analizó el comportamiento de la velocidad (Figura 3) y de la la altitud (Figura 4) de la fase propulsada.
Tal y como se puede observar en ambas figuras, la primera etapa alcanza valores de velocidad cercanos a los 2.7 km/s a una altura de 95 km. Al poner en funcionamiento la segunda etapa, el valor de la velocidad alcanza a llegar hasta los 8.3 km/s en el momento de su inserción a órbita (inyección) la cual se logra a una altura de 300 km al cabo de 459 segundos de fase propulsada.
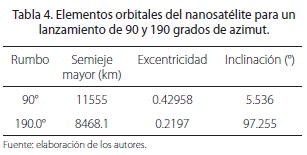
Lanzado a un azimut de 90 grados, el nanosatélite queda con una órbita cuasi ecuatorial, con una excentricidad bastante elevada (alturas de apogeo y perigeo de 10140 y 213 km), tal y como se puede observar en la primera línea de la Tabla 4. Es claro que el cohete está “energizado” en el sentido de que puede colocar en órbita masas un poco más grandes.
Un tipo de órbita bastante utilizada para efectos de recabar información de inteligencia, observación terrestre y reconocimiento es la denominada órbita solsincrónica. El hecho de que un satélite en este tipo de órbita sobrevuele, al cabo de cierto número de órbitas, por el mismo punto sobre la superficie terrestre bajo las mismas condiciones de iluminación solar, lo hace apropiado para cumplir las tareas mencionadas atrás (Portilla, 2009).
Para compensar el desplazamiento de la Tierra en dirección anti horaria a una tasa de casi un grado por día (debido a la traslación de la Tierra en torno al Sol) es preciso hacer que la línea de los nodos (que no permanece fija en el espacio a causa del armónico zonal J2), se desplace también en dirección anti horaria. Esto sólo se logra colocando el satélite en órbita cuasi polar, con una inclinación ligeramente superior a 90 grados, esto es, con una trayectoria en dirección contraria a la de la rotación de la Tierra.
Escogiendo valores convenientes de la inclinación, la excentricidad y el semieje mayor, es posible tener un margen de maniobra adecuado para lograr una tasa de desplazamiento del nodo en dirección anti horaria con un valor cercano al movimiento medio de la órbita terrestre de 0.98 grados por día.
La forma más obvia de colocar un satélite en órbita solsincrónica lanzado desde Gaori es dirigiendo el cohete con un azimut comprendido entre 96 y 100 grados, esto es, en dirección norte. Sin embargo, la trayectoria del cohete tendría el serio inconveniente de que sobrevolaría por zonas relativamente pobladas de la República Bolivariana de Venezuela, específicamente, estados como Portuguesa, Lara y Falcón los cuales tienen densidades poblacionales comprendidas entre 20 a 60 habitantes por km2.
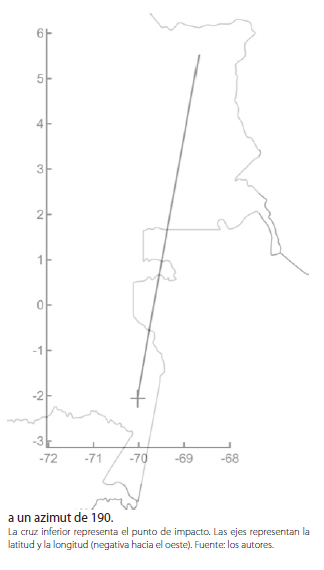
Por lo anterior, la alternativa más conveniente es lanzar el cohete con un azimut del orden de 190 grados, esto es, en dirección sur. De este modo, el cohete sobrevolaría regiones muy escasamente pobladas, tales como los departamentos de Vichada y Guainía (cuya densidad poblacional es del orden de 0.5 habitantes por km2) y una fracción del estado brasileño de Amazonas (densidad poblacional de 2 habitantes por km2) (ver Figura 5).
En la segunda línea de la Tabla 4, se registran los elementos orbitales de la carga útil para un lanzamiento de 190.0 grados y conservando las demás especificaciones de masas y tiempos de funcionamiento.
Conclusiones
El presente artículo hay que verlo como lo que es, un ejercicio académico tendiente a estudiar las trayectorias de vuelo de un posible cohete de construcción autóctona y de las órbitas de los satélites que sería capaz de situar en órbita. Estos satélites serían de bajas masas pero necesarios para satisfacer algunos requerimientos de la nación tanto militares como civiles.
No hay que dejar de lado el hecho de que la construcción de cohetes y satélites de forma autónoma por parte del país colocaría a Colombia como un actor a tener en cuenta en el escenario mundial y elevaría a niveles insospechados el orgullo nacional. Llevar esto a una realidad exige una enorme voluntad política, compromiso de Estado (no únicamente de Gobierno) y una fuerte movilización educacional e industrial, tal y como la que se llevó a cabo en los Estados Unidos a finales de la década de los años 50s en respuesta a la colocación del Sputnik I. Su implementación depende en esencia de la visión de la clase dirigente. De tomar la decisión, valdría la pena observar con detalle las experiencias actuales que se están llevando a cabo en Brasil y Argentina, países que están decididos a ser independientes en sus programas espaciales.
Por lo pronto, en este artículo hemos estudiado las trayectorias que tendría un cohete de dos etapas diseñado para colocar satélites pequeños en órbita variando el ángulo de azimut de lanzamiento. Para dicho estudio se optimizó la relación de masas y se integraron numéricamente las ecuaciones diferenciales de movimiento de un cohete por intermedio de códigos diseñados por los autores.
El código que se ha desarrollado para la realización de este análisis de trayectorias puede por entero modificarse para efectos de aplicarlo a todo tipo de cohetes que se puedan concebir, variando con facilidad los diversos parámetros de entrada y adaptándolo a nuestras necesidades y particularidades.
Con un lanzamiento del cohete desde la base de Gaori en el departamento del Vichada, se examinaron varios rangos de lanzamiento. El sitio es adecuado desde el punto de vista de la baja densidad poblacional, lo que permite minimizar los riesgos en caso de accidente o desperfecto. Sin embargo, para un amplio rango de azimuts, la trayectoría del cohete tendría que pasar por territorio venezolano. Más importante aun: la primera etapa, dependiendo del azimut, impactaría en zona continental de Venezuela, Guyana o Brasil o en la plataforma marítima de Venezuela. Esto evidentemente es un asunto sensible, por lo que su materialización dependería del estado de las relaciones de la nación con los países vecinos y, en el caso de que estén normalizadas, necesariamente desembocaría en una negociación (muy probablemente a través de compensaciones) para permitir que dichas naciones toleren el sobrevuelo y la caída de un artefacto (la estructura de la primera etapa) que representa un desperdicio y fuente de contaminación.
No tan sensible es un lanzamiento con valores de rumbo del orden de 190 grados o mayores. En tal caso, el cohete sobrevolaría la mayor parte del territorio colombiano (con una parte exigua de territorio brasileño) y la primera etapa caería en una zona de densa selva tropical al norte del departamento del Amazonas. Una trayectoria de este tipo sería utilizada en el caso de colocar satélites en órbitas solsincrónicas. Evidentemente, desde el punto de vista de no perturbar a las naciones vecinas ni incrementar los costos a través del pago de compensaciones, este tipo de órbitas serían las más convenientes.
Referencias
Fleeman, E. (2006). Tactical Missile Design. 2Ed. AIAA, Virginia.
Fostescue, P. Stark, J., y Swinerd, G. (2003). Spacecraft Systems Engineering. 3 Ed. Londres: Wiley.
Galli, P., y Rochus, S. (2008). Mision Design for the Cubesat OUTFI-1. Tesis en Ingeniería Civil – Electromecánica, Universidad de Liege.
Gutiérrez, R. (2012). Programa Espacial FAC, Avances y Proyección. Cuarto Congreso Colombiano en Ciencia y Tecnología Aeroespacial CICTA 2012. Bogotá: Universidad Distrital Francisco José de Caldas.
Humble, R., Henry, G., y Larson, W. (1995). Space Propulsion Analysis and Design. New York: Mc Graw Hill.
Joya, R. (2007). Desarrollo de Nuevas Tecnologías, Primer Satélite Colombiano en el Espacio, Libertad 1. Rev. Ciencia y Tecnología, Vol. 25 (2), pp. 46-51. Bogotá: Colciencias.
Minzner, R. A., Champion K.S.W., y Pond, H.L. (1959). The ARDC model atmosphere, 1959. Air Force Surveys in Geophysics N°115. Cambridge.
Portilla, J. (2009). Elementos de Astronomía de Posición. Bogotá: UNIBIBLOS.
Sutton, G., y Biblatz, O. (2010). Rocket Propulsion Elements, 8 Ed. New York: John Wiley and Sons.
Tewari, A. (2006). Atmospheric and Space Flight Dynamics. Berlín: Birkhauser.
Urrego, A. (2009). Investigaciones en Cohetería Experimental. Misión Séneca, Lanzamiento del Cohete Ainkaa 1. Tesis de Pregrado en Ingeniería Mecánica. Bogotá: Universidad de los Andes.
Weiland, C. (2010). Computational Space Flight Mechanics. Berlín: Springer
Zipfel, P. (2007). Modeling and Simulation of Aerospace Vehicle Dynamics. 2Ed. AIAA, Virginia.
________________________________________
5Reporte del 20 de junio de 2011 de la Asociación de Industra Satelital. [En línea] Disponible en www.sia.org.